1) pure predicate calculus of first order
一阶纯谓词演算
3) pure predicate calculus
纯谓词演算
4) second-order predicate calculus
二阶谓词演算
5) predicate calculus of the third order
三阶谓词演算
6) high-order predicate calculus
高阶谓词演算
补充资料：谓词演算
| 谓词演算 predicate calculus 数理逻辑最基本的形式系统。又称一阶逻辑。一个可以回答真假的命题，不仅可以分析到简单命题，还可以分析到其中的个体、量词和谓词。个体表示某一个物体或元素，量词表示数量，谓词表示个体的一种属性。例如用P(x)表示x是一棵树，则P(y)表示y是一棵树，用Q(x)表示x有叶，则Q(y)表示y也有叶。这里P、Q是一元谓词，x，y是个体，公式"x(P(x)→Q(x))表示每一棵树都有叶子，这里"是全称量词表示“每一个”。公式$x(P(x)∧  Q(x))表示有一棵没有叶的树，这里$是存在量词，表示“存在一个”。除了一元谓词，也可以有二元，三元，甚至多元谓词。事实上，数学中的关系，函数都可以看成谓词 。例如x≤y可以看成二元谓词，x＋y＝z可以看成三元谓词，因此谓词演算的公式可表示数学中的一些命题。例如若用Q(x)表示x是有理数，则公式(*)"x"y(Q(x)∧Q(y)∧x≤y→$z(Q(z)∧x＜z＜y)) 表示任意两个不相等的有理数中间一定存在另一个有理数。这就是有理数的稠密性。 谓词可以在一定的个体集合中给出解释，谓词公式可以在这样的个体集合中取到真假值。例如在实数集R中解释Q(x)为x是有理数，则谓词公式(*)取值为真。如果在R中解释Q(x)为“x是整数”，谓词公式(*)就取值为假了。谓词公式在个体集合中取值的严格定义称为基本语义定义，这个定义是波兰籍数学家A.塔尔斯基在20世纪30年代给出的。给定了谓词解释的个体集合称为模型。基本语义定义使谓词公式和模型都可以被当作数学对象加以研究。一个谓词公式在任意一个模型中都取真值，就称之谓恒真式。两个谓词公式A，B在任意模型的任何一种解释下都取相同的值，就称A，B逻辑等价。命题演算中的恒真式和等价式所反映的规律在谓词演算中仍成立。谓词演算中还有一些有关量词的等价式，如："xP(x)Û  $鰔 黀(x)，"x(j→ψ)Ûj→"xψ（x不在j中自由出现），"x(j→ψ)?xj→ψ（x不在ψ中自由出现）。利用这些有关量词的等价式作等价变换，可以把任何一个谓词公式的量词移到公式的最前面，得到与之等价的前束标准形公式。形如Qx1，Qx2，…，QxnB的公式称为前束型公式，其中Qxi表示$xi或"xi，B是一个不含量词的公式。谓词演算也研究谓词公式的推演。谓词演算自然推演的一些规则为： ①全称量词消去 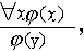  ②全称量词引入 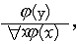 ③存在量词消去 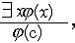 ④存在量词引入 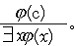  这些规则中横线上是条件，横线下是结论，j(x)是含自由变元x的谓词公式，y是不在j(x）中出现的变元，c是特定的个体常元，j(y)，j(c)是以y，c分别代替j(x)中所有自由出现的x得到的谓词公式。与命题公式的推演不同，谓词公式的推演要求条件是恒真式时得到的结论也是恒真式。谓词演算也可以公理化。从符号到公式的定义，从公理到推演都严格形式化，构成完全的公理系统，使系统所推演出的都是恒真式，且每个恒真式都能从公理推演出来。与命题演算不同的是，谓词演算是一个不可判定的系统，即不存在一个算法来判定谓词公式是否恒真式。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条