1) annotated predicate calculus(APC)
注解谓词演算
2) interpretation of predicate calculus
谓词演算的解释
3) predicate calculus
谓词演算
1.
Construction of predicate calculus finite set based on the requirement of management information ontology
管理信息本体需求的谓词演算有限集构造
2.
The safety of the system is analyzed with the predicate calculus.
本文基于模型驱动开发方法,使用结构分析和设计语言设计铁路平交道口控制系统,并使用谓词演算对系统的安全性进行分析,提高了系统的开发效率。
4) annotated predicate calculus
带注释的谓词演算
5) predicate m-calculus
谓词m演算
1.
The modal graphs are effective graph forms for the predicate m-calculus.
模态图是谓词m演算的一种有效的图形表示形式。
6) restricted predicate calculus
狭谓词演算
补充资料：谓词演算
| 谓词演算 predicate calculus 数理逻辑最基本的形式系统。又称一阶逻辑。一个可以回答真假的命题，不仅可以分析到简单命题，还可以分析到其中的个体、量词和谓词。个体表示某一个物体或元素，量词表示数量，谓词表示个体的一种属性。例如用P(x)表示x是一棵树，则P(y)表示y是一棵树，用Q(x)表示x有叶，则Q(y)表示y也有叶。这里P、Q是一元谓词，x，y是个体，公式"x(P(x)→Q(x))表示每一棵树都有叶子，这里"是全称量词表示“每一个”。公式$x(P(x)∧  Q(x))表示有一棵没有叶的树，这里$是存在量词，表示“存在一个”。除了一元谓词，也可以有二元，三元，甚至多元谓词。事实上，数学中的关系，函数都可以看成谓词 。例如x≤y可以看成二元谓词，x＋y＝z可以看成三元谓词，因此谓词演算的公式可表示数学中的一些命题。例如若用Q(x)表示x是有理数，则公式(*)"x"y(Q(x)∧Q(y)∧x≤y→$z(Q(z)∧x＜z＜y)) 表示任意两个不相等的有理数中间一定存在另一个有理数。这就是有理数的稠密性。 谓词可以在一定的个体集合中给出解释，谓词公式可以在这样的个体集合中取到真假值。例如在实数集R中解释Q(x)为x是有理数，则谓词公式(*)取值为真。如果在R中解释Q(x)为“x是整数”，谓词公式(*)就取值为假了。谓词公式在个体集合中取值的严格定义称为基本语义定义，这个定义是波兰籍数学家A.塔尔斯基在20世纪30年代给出的。给定了谓词解释的个体集合称为模型。基本语义定义使谓词公式和模型都可以被当作数学对象加以研究。一个谓词公式在任意一个模型中都取真值，就称之谓恒真式。两个谓词公式A，B在任意模型的任何一种解释下都取相同的值，就称A，B逻辑等价。命题演算中的恒真式和等价式所反映的规律在谓词演算中仍成立。谓词演算中还有一些有关量词的等价式，如："xP(x)Û  $鰔 黀(x)，"x(j→ψ)Ûj→"xψ（x不在j中自由出现），"x(j→ψ)?xj→ψ（x不在ψ中自由出现）。利用这些有关量词的等价式作等价变换，可以把任何一个谓词公式的量词移到公式的最前面，得到与之等价的前束标准形公式。形如Qx1，Qx2，…，QxnB的公式称为前束型公式，其中Qxi表示$xi或"xi，B是一个不含量词的公式。谓词演算也研究谓词公式的推演。谓词演算自然推演的一些规则为： ①全称量词消去 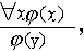  ②全称量词引入 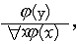 ③存在量词消去 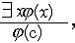 ④存在量词引入 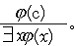  这些规则中横线上是条件，横线下是结论，j(x)是含自由变元x的谓词公式，y是不在j(x）中出现的变元，c是特定的个体常元，j(y)，j(c)是以y，c分别代替j(x)中所有自由出现的x得到的谓词公式。与命题公式的推演不同，谓词公式的推演要求条件是恒真式时得到的结论也是恒真式。谓词演算也可以公理化。从符号到公式的定义，从公理到推演都严格形式化，构成完全的公理系统，使系统所推演出的都是恒真式，且每个恒真式都能从公理推演出来。与命题演算不同的是，谓词演算是一个不可判定的系统，即不存在一个算法来判定谓词公式是否恒真式。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条