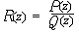2) Meromorphic function


亚纯函数
1.
On an uniqueness of meromorphic functions sharing two finite sets;


关于分担两个集合的亚纯函数的唯一性
2.
Uniqueness of meromorphic functions concerning weakly weighted-sharing small functions;


涉及权弱分担小函数的亚纯函数唯一性
3.
Uniqueness theorem of meromorphic functions sharing one value;


权分担一个值的亚纯函数的唯一性定理
3) meromorphic
[,merə'mɔ:fik]


亚纯函数
1.
The problem of uniqueness of meromorphic functions is discussed.


讨论了亚纯函数的惟一性问题,证明存在一个具有12个元素的集合S使得对任意2个非常数的亚纯函数f与g,只要满足3)(S,f)=3)(S,g)和({∞},f)=({∞},g),必有f≡g。
2.
We will give reduce demonstration for a lemma in four values theorem of meromorphic function.
给出了亚纯函数四值定理中一个引理的简化证明。
3.
In this paper we get the following results: Let (z) be a meromorphic function in domain G which is not identically zero, a1(z), a2(z), …,ak(z) be holomorphic function in domain G, F={f} be a family of meromorphic functions in G.
本文获得如下结果:设(z)为区域G内一不恒为零的亚纯函数,a1(z),a2(z),…,ak(z)为区域G内的全纯函数,F={f}为G内一亚纯函数族。
4) meromorphic mapping


亚纯映射
1.
Uniqueness theorem of meromorphic mappings intersecting hypersurfaces;


亚纯映射相交超曲面的唯一性定理
2.
Based on the study of the relation between meromorphic mapping and moving targets,a new truncated second main theorem is proved for meromorphic mapping in several complex variables with moving targets.
通过对亚纯映射与小映射之间关系的研究,给出了一个涉及小映射的亚纯映射精简密指量形式的第二基本定理,并由此得到相应的亚纯映射唯一性定理。
3.
The object of this thesis is to study the uniqueness problems of meromorphic func-tions and meromorphic mappings in several complex variables.
本文以多复变数的亚纯函数与亚纯映射的唯一性问题为研究对象。
5) mermorphic function


亚纯函数
1.
Normal families of mermorphic function concerning differential monomials


涉及微分多项式的亚纯函数的正规族
2.
In this dissertation, we study normal families of mermorphic functions, which is an important subject in complex analysis.
本文主要研究亚纯函数族的正规性问题。
6) meromorphic continuity


亚纯连续