1) meromorphic differential


亚纯微分
2) holomorphic differential


全纯微分
3) pure differential form


纯微分式
4) factorization of function


亚纯函数的分解
5) holomorphic quadratic differentials


全纯二次微分
1.
As an application of this, the relationship between the Teichmüller metric in T_g and the norm in the space QD(σ) of holomorphic quadratic differentials on (M,σdz~2) is obtained.
作为其应用,建立起Tg中的Teichmüller度量与(M,σdz2)上的全纯二次微分空间QD(σ)中的范数之间的联系。
6) holomorphic differential form


全纯微分形式
补充资料:亚纯函数
| 亚纯函数 meromorphic function 在区域D上有定义 ,且除去极点之外处处解析的函数。比如有理函数就是在扩充复平面上的亚纯函数,它是两个多项式的商 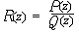 ,而Q(z)的零点是R(z)的极点 ,即R(z)有有限多个极点,∞点是R(z)的极点或可去奇点 。复平面上不是有理函数的亚纯函数称为超越亚纯函数。例如ctgz就是超越亚纯函数 ,它以kπ为全部极点 ,超越亚纯函数一定有无限多个极点。有理函数可以分为部分分式,即 
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |