1) homotopy group functor
同伦群函子
2) homotopy functor
同伦函子
3) homotopy epimorphism functor
同伦满函子
1.
This paper gives some properties of homotopy regular morphisms,defines homotopy epimorphism functor and homotopy monomorphism functor,it also proves that these two functors preserve the properties of homotopy regular.
本文给出了同伦正则态射的一些性质,定义了同伦满函子和同伦单函子,证明了这两类函子保持同伦正则性。
4) homotopy monomorphism functor
同伦单函子
1.
This paper gives some properties of homotopy regular morphisms,defines homotopy epimorphism functor and homotopy monomorphism functor,it also proves that these two functors preserve the properties of homotopy regular.
本文给出了同伦正则态射的一些性质,定义了同伦满函子和同伦单函子,证明了这两类函子保持同伦正则性。
5) homotopy function
同伦函数
1.
A mathematical model to analyze power system frequency where wind farms are involved is built,and by use of homotopy function the state variables corresponding to system eigenvalues are discriminated,especially the state variables related to system frequency.
建立了一种含风电场的电力系统频率分析数学模型,利用同伦函数辨别出系统特征值对应的状态变量,特别是与系统频率相关的状态变量。
6) Group homotopy inverse
群同伦逆
补充资料：同伦群
| 同伦群 homotopy group 代数拓扑的概念。设f和g是拓扑空间X到Y的两个连续映射，如果能通过连续形变将f变为g ，则称f与g同伦。精确地说，如果存在连续映射H∶X×〔0，1〕→Y，使对任意x∈X，H（x，0）＝f（x），H（x，1）＝g（x），则称f同伦于g。a，β∶Sn→X是两个连续映射 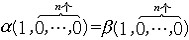 ＝x0∈X，如果a和β保持x0不动地由一个形变到另一个则称a与β保持基点x0同伦 ，记作a～x 0β。用G（X，x0）记满足a（1，0，…0）＝x0的连续映射a∶Sn→X的全体作成的集合。～x0是其上的等价关系 ，则商群G（X，x0）／～x0称为X的以x0为基点的n维同伦群，记作πn（X，x0）＝G（X，x0）／～x0 。n＝1时称为X的以x0为基点的基本群。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条