1) associative law for series


级数的结合律
2) associative law


结合律
1.
In this paper,the authors give a new multiplication of the cubic matrices,and testify the associative law and the distributive law of the new multiplication are right under the new multiplication.
给出了立体阵乘法的一个新定义,推导出新乘法满足分配律和结合律;并且给出了立体阵的转置矩阵的定义,得到了立体阵的转置矩阵的一些性质。
2.
This paper deals with the relation between the associative law of binary operations and the power xn and the inverse x-1 of an element x.
本文讨论了二元运算的结合律与元素的乘幂和逆元的关系,探讨了命题逻辑联结词运算的结合律,得到几个有意义的结果,拓展了当前离散数学教材中相应知识点的内容。
3.
The note gives some examples on a set with two binary operations which satisfying, or unsatisfying, respectively, the commutative law, the associative law and the distributive law; and discusses the examples satisfying n -element distributive law but not satisfying (n-1) -element distributive law.
给出一个集合上的两个 (二元 )代数运算分别满足或不满足交换律、结合律和分配律的各类例子 ,同时给出了n元分配律成立而 n-1元分配律不成立的例子 。
3) associative law of ring


环结合律
4) the Rationality of legal criterion structure


法律规范结构的合理性
5) combinatorial analysis of primary structure database of proteins


蛋白质一级序列结构数据库的组合图论分析
6) twisted generalized power series ring


带扭结的广义幂级数环
补充资料:级数
| 级数 series 将数列un的项 u1,u2,…,un,…依次用加号连接起来的函数。数项级数的简称。如:u1+u2+…+un+…,简写为  un称为级数的通项,记 un称为级数的通项,记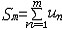 称之为级数的部分和。如果当m→∞时 ,数列Sm有极限S,则说级数收敛,并以S为其和,记为 称之为级数的部分和。如果当m→∞时 ,数列Sm有极限S,则说级数收敛,并以S为其和,记为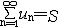 否则就说级数发散。级数是研究函数的一个重要工具,在理论上和实际应用中都处于重要地位,这是因为:一方面能借助级数表示许多常用的非初等函数, 微分方程的解就常用级数表示;另一方面又可将函数表为级数,从而借助级数去研究函数,例如用幂级数研究非初等函数,以及进行近似计算等。级数的收敛问题是级数理论的基本问题。从级数的收敛概念可知,级数的敛散性是借助于其部分和数列Sm的敛散性来定义的。因此可从数列收敛的柯西准则得出级数收敛的柯西准则 : 否则就说级数发散。级数是研究函数的一个重要工具,在理论上和实际应用中都处于重要地位,这是因为:一方面能借助级数表示许多常用的非初等函数, 微分方程的解就常用级数表示;另一方面又可将函数表为级数,从而借助级数去研究函数,例如用幂级数研究非初等函数,以及进行近似计算等。级数的收敛问题是级数理论的基本问题。从级数的收敛概念可知,级数的敛散性是借助于其部分和数列Sm的敛散性来定义的。因此可从数列收敛的柯西准则得出级数收敛的柯西准则 :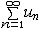 收敛 收敛 任意给定正数ε,必有自然数N,当n>N时 ,对一切自然数 p,有|un+1+un+2+…+un+p|<ε,即充分靠后的任意一段和的绝对值可任意小。 任意给定正数ε,必有自然数N,当n>N时 ,对一切自然数 p,有|un+1+un+2+…+un+p|<ε,即充分靠后的任意一段和的绝对值可任意小。如果每一un≥0(或un≤0),则称 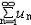 为正(或负)项级数,正项级数与负项级数统称为同号级数。正项级数收敛的充要条件是其部分和序列Sm 有上界,例如 为正(或负)项级数,正项级数与负项级数统称为同号级数。正项级数收敛的充要条件是其部分和序列Sm 有上界,例如  收敛,因 为 收敛,因 为 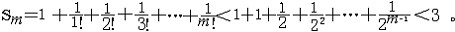 有无穷多项为正,无穷多项为负的级数称为变号级数,其中最简单的是形如 有无穷多项为正,无穷多项为负的级数称为变号级数,其中最简单的是形如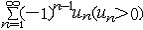 的级数,称之为交错级数。判别这类级数收敛的基本方法是莱布尼兹判别法 :若un ≥un+1 ,对每一n∈N成立,并且 的级数,称之为交错级数。判别这类级数收敛的基本方法是莱布尼兹判别法 :若un ≥un+1 ,对每一n∈N成立,并且 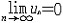 ,则交错级数收敛。例如 ,则交错级数收敛。例如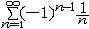 收敛。对于一般的变号级数如果有 收敛。对于一般的变号级数如果有 收敛,则称变号级数绝对收敛。如果只有 收敛,则称变号级数绝对收敛。如果只有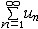 收敛,但是 收敛,但是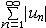 发散,则称变号级数条件收敛。例如 发散,则称变号级数条件收敛。例如 绝对收敛,而 绝对收敛,而 只是条件收敛。 只是条件收敛。 如果级数的每一项依赖于变量 x,x 在某区间I内变化,即un=un(x),x∈I,则称  为函数项级数,简称函数级数。若x=x0使数项级数 为函数项级数,简称函数级数。若x=x0使数项级数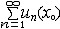 收敛,就称x0为收敛点,由收敛点组成的集合称为收敛域,若对每一x∈I,级数 收敛,就称x0为收敛点,由收敛点组成的集合称为收敛域,若对每一x∈I,级数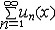 都收敛,就称I为收敛区间。显然,函数级数在其收敛域内定义了一个函数,称之为和函数S(x),即 都收敛,就称I为收敛区间。显然,函数级数在其收敛域内定义了一个函数,称之为和函数S(x),即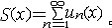 如果满足更强的条件, 如果满足更强的条件, 在收敛域内一致收敛于S(x)。 在收敛域内一致收敛于S(x)。一类重要的函数级数是形如 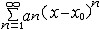 的级数,称之为幂级数 。它的结构简单 ,收敛域是一个以 的级数,称之为幂级数 。它的结构简单 ,收敛域是一个以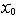 为中心的区间(不一定包括端点),并且在一定范围内具有类似多项式的性质,在收敛区间内能进行逐项微分和逐项积分等运算。例如幂级数 为中心的区间(不一定包括端点),并且在一定范围内具有类似多项式的性质,在收敛区间内能进行逐项微分和逐项积分等运算。例如幂级数 的收敛区间是 的收敛区间是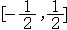 ,幂级数 ,幂级数 的收敛区间是[1,3],而幂级数 的收敛区间是[1,3],而幂级数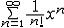 在实数轴上收敛。 在实数轴上收敛。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条