1) anharmonic vibration


非谐振动
2) anharmonic vibration


非简谐振动
1.
The influence of the anharmonic vibration on the expansion coefficient and elastic modulus has been discussed in this article with the examples of Ag,Cu and Ni which have the fcc structures.
以面心立方金属晶体Ag,Cu,Ni为例,讨论了非简谐振动对晶体的热膨胀系数、固体弹性模量的影响。
2.
Considering atomic anharmonic vibration,the authors figure out the free energy of granule and the harmonic parameter and anharmonic parameter of atomic vibration of single-domain ferromagnetic in uniform external field.
在考虑到原子作非简谐振动的情况下,先求出在均匀外磁场中单轴铁磁粒子原子振动的简谐系数、非简谐系数和粒子的自由能。
3.
By taking Fe as an example, we discuss the influences of anharmonic vibration on the thermal capacity and the resistivity of Fe, and draw a conclusion that when coinciding the influence of anharmonic vibration the theory result is close to the experiment.
以铁为例,讨论了原子非简谐振动对晶体的定压热容量和电阻率的影响。
3) anharmonicy


非简谐振动势
4) damped non-harmonic vibration


阻尼非简谐振动
5) non-harmonic oscillator


非谐振子
1.
Generalized coherent states and exact solutions of parameter q non-harmonic oscillator;


非谐振子q变形下的广义相干态与精确解
2.
The ionic of univalent ionic crystals is dealt with as non-harmonic oscillator, revised value of perturbation term on energy level is obtained by using perturbation theory.
将单价离子晶体的离子进行非谐振子处理,利用微扰理论求解微扰项对能级的修正值,与经典结果比较,这种量子方法计算出的单价离子晶体结合能更为精确。
3.
A class non-harmonic oscillator whose perturbation term is lXHl= is discussed by using coherent state and normal product.
利用相干态和正规乘积对一类微扰项为XHl=的非谐振子进行了讨论,得到了H矩阵元的精确解和H对非谐振子能级的一级修正值,为处理非谐振子的微扰问题提供了一种新的方法。
6) anharmonic oscillator


非谐振子
1.
Gazeau-Klauder and Klauder-Perelomov coherert states for the anharmonic oscillator;


非谐振子Gazeau-Klauder与Klauder-Perelomov相干态
2.
The energy spectra and eigenstates of an anharmonic oscillator for the bound states is studied with the aid of pseudo_angular_momentum method.
采用赝角动量的方法研究了非谐振子定态薛定谔方程的严格解 。
3.
Nonclassical properties of the generalized Gazeau-Klauder coherent state are investigated for an anharmonic oscillator.
研究了非谐振子广义Gazeau-Klauder相干态的非经典特性,对Mandel Q参量的二阶相关函数的计算表明:GK相干态服从亚泊松统计分布且具有反聚束效应。
补充资料:简谐振动
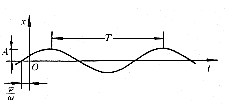
| 简谐振动 simple harmonic vibration 描述系统状态的物理量随时间按正弦或余弦规律作周期性变化的过程。又称简谐运动。作简谐振动的物体的加速度始终同它的位移成正比,但方向相反。即x=-ω2x, 式中ω2为比例常量。作简谐运动的物体,其运动规律可表达为: x=Asin(ωt+ 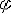 ) )=Asin(2πt/T+ 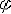 ) )=Asin(2πf t+ 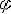 ) )式中x为位移;A为振幅;ω为角(圆)频率;t为时间;T为周期;f 为频率;ωt+ 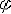 为相位 ; 为相位 ;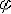 为初相位(见图)。这种运动对其平衡位置(零点)是对称的。在零点上,物体速度最大,加速度为零;在最大位移处(转向点),速度为零,加速度最大。简谐运动是最简单、最基本的振动形式;任何周期振动都可由许多不同频率和振幅的简谐运动合成。简谐运动是单自由度无阻尼系统微幅自由振动的抽象模型。悬挂在弹簧下端物体的微幅振动,扭摆的微幅振动以及晶体中原子围绕平衡位置的微幅振动都可近似地看作简谐振动。 为初相位(见图)。这种运动对其平衡位置(零点)是对称的。在零点上,物体速度最大,加速度为零;在最大位移处(转向点),速度为零,加速度最大。简谐运动是最简单、最基本的振动形式;任何周期振动都可由许多不同频率和振幅的简谐运动合成。简谐运动是单自由度无阻尼系统微幅自由振动的抽象模型。悬挂在弹簧下端物体的微幅振动,扭摆的微幅振动以及晶体中原子围绕平衡位置的微幅振动都可近似地看作简谐振动。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条