1) generalized dissipation


广义耗散
2) generalized dissipation force


广义耗散力
1.
The author provides a definition of the dissipation function from which the generalized dissipation force is derived.
本文作者首先定义出耗散函数 ,由耗散函数导出广义耗散力 ,然后建立含耗散函数的拉格朗日方程 ;最后讨论耗散函数的物理意义。
3) constrained generalized Hamiltonian system


耗散广义Hamilton约束系统
1.
For the constrained generalized Hamiltonian system with dissipation, by introducing Lagrange multiplier and using projection technique, the Lie group integration method was presented, which can preserve the inherent structure of dynamic system and the constraint-invariant.
针对耗散广义Hamilton约束系统,通过引入拉格朗日乘子和采用投影技术,给出了一种保持动力系统内在结构和约束不变性的李群积分法· 首先将带约束条件的耗散Hamilton系统化为无约束广义Hamilton系统,进而讨论了无约束广义Hamilton系统的李群积分法,最后给出了广义Hamilton约束系统李群积分的投影方法· 采用投影技术保证了约束的不变性,引入拉格朗日乘子后,在向约束流形投影时不会破坏原动力系统的李群结构· 讨论的内容仅限于完整约束系统,通过数值例题说明了方法的有效性·
4) weakly dissipative generalized C-H equation


弱耗散的广义C-H方程
5) generalized dissipative Camassa-Holm equations


广义耗散Camassa-Holm方程
1.
The peakons and their figures of the GCH equation are given with the Mathematic software for m -1 , m = 2 and m = 3 in particular ; For m=3, I get the generalized dissipative Camassa-Holm equations by adding a dissipative term and find two types exact traveling wave solutions of this equations.
本文研究广义Camassa-Holm(GCH)方程的行波孤立子解及尖峰孤立子解,给出GCH方程的行波孤立子解的表达式,特别的,对m=1、m=2、m=3时利用Mathematica数学软件进行计算,解出了GCH方程的尖峰孤立子解,并给出了此时GCH方程的尖峰孤立子解的图形,使数值分析和理论相结合;对m=3时的GCH方程增加一耗散项εu_(xx)后得到广义耗散Camassa-Holm方程,并解出此方程的两类精确行波解;本文将齐次平衡法应用到GCH方程中,解出m=2、m=3时的GCH方程的一组光滑解,同时应用此方法得到了m=3时的GCH方程的Backlund变换。
6) generalized energy consumption


广义能耗
补充资料:广义力
| 广义力 generalized force 与广义坐标qi对应的力,它的量纲由它与qj的虚位移δqj的乘积为功的物理量决定。若δqj为线位移,则广义力就是作用力;若  qi为角位移,则广义力就是力矩。广义力的定义也可以从坐标变换式得来,即 qi为角位移,则广义力就是力矩。广义力的定义也可以从坐标变换式得来,即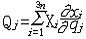 (j=1,2…,N),式中Xi为xi方向的作用力;Qj 为与广义坐标qj对应的广义力。N自由度的完整系统(见约束)有N个广义力。对于N自由度的完整保守系统 ,存在势函数V (q1,q2,…qN) 。由于 (j=1,2…,N),式中Xi为xi方向的作用力;Qj 为与广义坐标qj对应的广义力。N自由度的完整系统(见约束)有N个广义力。对于N自由度的完整保守系统 ,存在势函数V (q1,q2,…qN) 。由于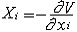 ,所以广义力 ,所以广义力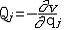 (j=1,2…,N)。用广义力和广义坐标表示的虚位移原理为: (j=1,2…,N)。用广义力和广义坐标表示的虚位移原理为: 。由于δqj的独立性,上式等价于 Qj=0(j=1,2,…N,),即理想完整约束系统平衡的必要和充分条件是全部广义力等于零。 。由于δqj的独立性,上式等价于 Qj=0(j=1,2,…N,),即理想完整约束系统平衡的必要和充分条件是全部广义力等于零。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条