1) Banach space


巴拿来赫空间
2) banach space


巴拿赫空间
1.
Fixed points of a nonexpansive mapping in a Banach space;


巴拿赫空间中不放大映射的不动点
2.
Reproof of function Space L~p being Banach space;


再证函数空间L~p是巴拿赫空间
3.
By using of the moment inequalities for B-valued random variables and Etemandi inequality,we not only generalize the main results of Chen[1] and Sung[3](2005) to Banach space,but also weaken the condition of their results.
通过使用一些关于B值独立随机变量的矩不等式和Etemandi不等式,把主要结果从实值情况推广到了P(1≤P≤2)型的巴拿赫空间中,并且将定理条件进行了极大的简化。
3) Banach spaces


巴拿赫空间
1.
Further discusses nonlinear ω semigroups in Banach spaces, and obtains some its properties, and extends some conclusions on semigroups of nonlinear contractions.
在巴拿赫空间上进一步研究非线性 ω型半群 ,得到它的一些性质 ,推广了非线性压缩半群的有关结
2.
Proves that in any infinite dimensional Banach spaces there exist two closed subspaces,which sum isnt closed.
证明了在任一无限维巴拿赫空间中,都存在其和不闭的两个闭子空间,并给出判定巴拿赫空间中两个闭子空间和的闭性的系列准则。
4) quotient Banach space


商巴拿赫空间
1.
Theory of Fredholm complexes on quotient Banach spaces;


商巴拿赫空间上的Fredholm复形理论
5) WCD Banach space


WCD巴拿赫空间
1.
If X is WCD Banach space then a projectional resolution of identity on X is constructed and dual projectous form resotution of identity on X~*.
若X是-WCD巴拿赫空间,则在X上可构造一单位射影分解,而其对偶射影形成X上一单位射影分解。
6) Σ1e type space


Σ1e型巴拿赫空间
补充资料:巴拿赫空间
| 巴拿赫空间 Banach space 赋予范数的完备的线性空间。范数是通常熟悉的长度概念的拓广。 一个数域 K上的线性空间X,如有从X到R的函数‖·‖,满足:‖x‖≥0,‖x‖=0Ûx为零元;‖a x‖=|a|‖x‖, 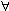 a ∈K; ‖x+y‖ ≤ ‖x‖ + ‖y‖ ,则称‖·‖为X上的一个范数。例如在R中,让每一元x与‖x‖=|x|对应,这里|x|表示通常的绝对值,则‖·‖为R 上的一个范数。 又如,设 X ={f:f为定义在 [a, b] 上的连续函数},在X中引入加法和数乘如下: a ∈K; ‖x+y‖ ≤ ‖x‖ + ‖y‖ ,则称‖·‖为X上的一个范数。例如在R中,让每一元x与‖x‖=|x|对应,这里|x|表示通常的绝对值,则‖·‖为R 上的一个范数。 又如,设 X ={f:f为定义在 [a, b] 上的连续函数},在X中引入加法和数乘如下: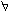 f,g∈x,(f+g)(t)=f(t)+g(t),(a f)(t)=a·f(t),则 X成为线性空间,又对每一f ∈X,定义 f,g∈x,(f+g)(t)=f(t)+g(t),(a f)(t)=a·f(t),则 X成为线性空间,又对每一f ∈X,定义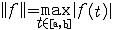 ,则可以验证‖·‖为X上的一个范数,故X是线性赋范空间,并且每一{fn}ÌX,若其为基本列,即‖fm-fn‖→0,则必有f ∈x,使‖fn-f‖→0。所以X是巴拿赫空间。巴拿赫空间是泛函分析研究的基本空间之一。自 1922年提出巴拿赫空间的概念,尤其是自1932年,S.巴拿赫的著作《线性算子理论》问世以后,人们对巴拿赫空间理论进行了系统深入的研究,60年代以来,取得迅速发展,许多问题得到了解决。最重要的成果之一是1973年P.恩夫洛给出了例子,表明可分的巴拿赫空间不一定有基,从而对巴拿赫的古典问题以否定的回答。此外,人们从不同的角度和需要,对巴拿赫空间的理论进行了广泛深入的研究,如对偶理论、各种收敛性、算子谱论等,使巴拿赫空间的理论日臻完善,并得到多方面的广泛应用。 ,则可以验证‖·‖为X上的一个范数,故X是线性赋范空间,并且每一{fn}ÌX,若其为基本列,即‖fm-fn‖→0,则必有f ∈x,使‖fn-f‖→0。所以X是巴拿赫空间。巴拿赫空间是泛函分析研究的基本空间之一。自 1922年提出巴拿赫空间的概念,尤其是自1932年,S.巴拿赫的著作《线性算子理论》问世以后,人们对巴拿赫空间理论进行了系统深入的研究,60年代以来,取得迅速发展,许多问题得到了解决。最重要的成果之一是1973年P.恩夫洛给出了例子,表明可分的巴拿赫空间不一定有基,从而对巴拿赫的古典问题以否定的回答。此外,人们从不同的角度和需要,对巴拿赫空间的理论进行了广泛深入的研究,如对偶理论、各种收敛性、算子谱论等,使巴拿赫空间的理论日臻完善,并得到多方面的广泛应用。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条