1) vector-valued random power series on the unit ball of C~n


C~n单位球上的向量值随机幂级数
2) vector valued random power series in several complex variables


向量值多复变随机幂级数
1.
We introduce the definition of vector valued random power series in several complex variables,and study its convergence.
引入了向量值多复变随机幂级数的定义 ,研究了它的收敛性质 ,它是Salem Zygmund定理的推广 。
3) Unit ball of C~n


C~n中的单位球
4) random power series


随机幂级数
1.
In this paper,we study the growth of random power series whose coefficients norms are pairwise NQD sequences.
本文研究了系数的模为两两NQD序列的B-值随机幂级数的增长性。
2.
In this paper,we study little α-Bloch spaces and random power series ∑α≥0εαaαzα in the unit ball,and give certain sufficient condition for ∑α≥0εαaαzα to belong to little α-Bloch spaces.
讨论了单位球上小α-Bloch空间与随机幂级数∑α≥0εαaαzα,得到了随机幂级数∑α≥0εαaαzα属于小α-Bloch空间的一个充分条件。
3.
We discuss complex function spaces and random power series fω(z),and give sufficient conditions for an analytic function belonging to Besov spaces Bp.
Anderson较为系统的研究了Bloch空间和随机幂级数fω(z),得到了fω(z)几乎必然地属于Bloch空间的充分但非必要条件。
5) power unit vector


幂单位向量
1.
On the power unit vector presented by Yang Wenxiong, it for the mathematical theory of k multiplier is extended to create a new mathematical branch.
在杨文熊提出的幂单位向量的基础上 ,推广其为k乘子的数学理论并由此建立了一门新的数学分支· 推广的k乘子还涉及到它的负整数幂· 列举了由k乘子组成的复合变数及其函数都能满足由杨文熊在“幂向量 ,复合向量数及其函数理论”中导出的各种条件、定理、积分以及方程等· k乘子理论将进一步应用于建立粒子超光速理论以及自然的波粒二象性运动的研究·
6) power series with random coefficients


随机系数幂级数
补充资料:幂级数
| 幂级数 power series 一个无穷阶的多项式。又称为泰勒级数。它的一般形式是a0+a1(z-z0)+…+an(z-z0)n+…=  ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。 ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。有一种幂级数 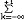 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有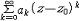 在圆|z-z0|<R上收敛,且 r<R,则级数 在圆|z-z0|<R上收敛,且 r<R,则级数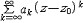 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形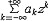 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条