1) parabolic equation approximation


抛物方程近似
1.
In this thesis, parabolic equation approximation, FOR3D, is used .


本论文利用抛物方程近似,FOR3D程序来研究内波对声传播的影响。
2) parabolic similar equation


抛物近似方程
1.
The transmission loss patterns of the electromagnetic field was studied by solving the parabolic similar equation which is gotten from the Helmholtz equation similarly.
运用电磁波场基本理论,推导了海气界面的电磁波场散射方程;通过对由Helmholtz方程近似得到的抛物近似方程的求解,研究了海气界面上电磁波的传播损耗模式,探讨了电磁波在海气界面的蒸发波导中的传播模型;采用双尺度模型,并根据海面微尺度波谱和Bragg散射理论建立了海浪谱与雷达散射截面的关系。
3) higher order approximation parabolic mild slope equation


高阶近似抛物缓坡方程
1.
A random wave model combining wave refraction and diffraction has been developed,which is based on the higher order approximation parabolic mild slope equation and uses the linear superposition theory.
文章基于高阶近似抛物缓坡方程 ,利用线性叠加原理建立了自然地形条件下综合考虑水波折射、绕射的随机波模型。
4) parabolic approximation


抛物线近似
1.
Through using parabolic approximation and linear approximation together, sine function signal is approximated with highly accuracy.
通过联合运用抛物线近似和线性近似实现了对正弦信号的高精度近似,所产生的最大谐波电平为-56。
5) approximate equation


近似方程
1.
A basic method is given to evaluate its material and energy, and a group of approximate equation can be obtained and a precision solution can also be attainable.
文中给出了该流程物料衡算和能量计算的基本方法,得到了1组近似方程,可用于编程运算求出其精确解。
2.
Chen s approximate equation is better than some others equation that pointed out in this paper.
在换热器的设计及换热系统网络优化中, 对数平均温度差( LMTD) 的计算有十分重要的意义- 本文对已提出的近似方程代替对数平均温度差的计算方法进行了评价, 指出J。
6) parabolic equation


抛物方程
1.
Application of the wide-angle parabolic equation under impedance boundary condition;


宽角抛物方程在阻抗边界条件下的应用
2.
Blow-up of nonnegative radial solutions for a family of parabolic equations in bounded domain in RN;
R~N中有界域上的一类抛物方程非负径向解的爆破问题
3.
Renormalized solutions of a class of strongly degenerate quasilinear parabolic equations;


一类强退化拟线性抛物方程的重整化解
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 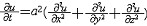 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式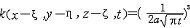 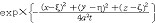 热传导方程初值问题的解可用基本解叠加而成,即 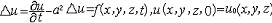 的解为 的解为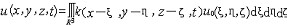 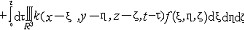 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 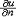 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条