1) parabolic rotation hypersurface


抛物型旋转超曲面
1.
We study the parabolic rotation hypersurfaces M~n whose coordinate functions are proper functions of their Laplacians in (n+1)-dimensional pseudo-Riemannian space forms.
研究n+1维伪黎曼空间型(?)~(n+1)(c)中坐标函数是其Laplacian的特征函数的抛物型旋转超曲面M~n,得到M~n为极小或极大超曲面,并给出了M~n的位置向量场。
2) parabolic rotation surface


抛物型旋转曲面
1.
In the 3-dimensional de (?)itter space,parabolic rotation surfaces with constant mean curvature(nonzero)were classified.
本文讨论三维 de sitter 空间中的曲面,得到了具有非零常平均曲率的所有抛物型旋转曲面,给出它们的方程。
3) parabolic quadratic hypersurface


抛物型二次超曲面
4) parabolic surfaces


抛物型曲面
1.
Correspondingly the definitions ofthree kinds of curved surfaces are given, that is the definitions of elliptic surfaces,hyperbolic surfaces and parabolic surfaces.
具体介绍了由圆锥曲线的轨迹生成的三类曲纹曲面——椭圆型曲面、双曲型曲面和抛物型曲面。
5) rotation hypersurface


旋转超曲面
1.
By introducing the concept of rotation hypersurfaces in pseudo-Riemannian space form and computing their principal curvatures, we obtain the existence theorem of rotation Weingarten hypersurfaces in pseudo-Riemannian space form.
通过引入伪黎曼空间型中旋转超曲面的概念,并给出其主曲率计算公式,得到伪黎曼空间型中旋转型Weingarten超曲面的存在性定理。
2.
The spherical,hyperbolic and parabolic spacelike or timelike rotation hypersurfaces whose coordinate functions are proper functions of their Laplacians in 4-dimensional anti-de Sitter space are studied.
研究伪欧氏空间E52中反de S itter空间H41的坐标函数是其Lap lac ian的特征函数的球型、双曲型和抛物型类时和类空旋转超曲面M的性质,得到:M或者为H41的极小或极大超曲面,或者可与某个乘积流形叠合。
3.
In particular, rotation hypersurfaces of finite type are studied and classified.


本文定义了伪黎曼空间型中的旋转超曲面,并给出其参数表达式及主曲率计算公式。
6) rotating parabolic antenna


旋转抛物面天线
1.
Simulation and analysis of the rotating parabolic antenna features based on Matlab


基于Matlab的旋转抛物面天线几种特性的仿真分析
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 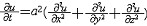 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式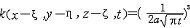 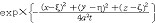 热传导方程初值问题的解可用基本解叠加而成,即 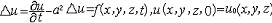 的解为 的解为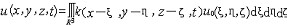 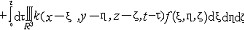 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 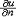 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条