1) Gauss rounding function


Gauss取整函数
1.
Using the elementary method and the properties of the Gauss rounding function,the real number solutions of an equation xy=|x-y| are studied,and its all real number solutions are obtained.
利用初等方法及Gauss取整函数[x]的性质研究方程x[y]-[x]y=|x-y|的可解性,并给出它的所有实数解。
2) integral function


取整函数
1.
Some probabilistic properties of integral function are discussed and some decomposition methods of non-negative random variable are proved.
通过讨论取整函数的几个概率性质,证明了对非负随机变量的取整函数分解方法,并把这种分解方法用于纺织纤维加工工艺中纱条牵切前后纤维长度分布之间关系的分析中。
2.
The paper discusses several analytic characters and the extensive application of the integral function and fraction parts of functions,which have the differentiation with contact.
取整函数与小数部分函数既相互联系又有区别,各有一些独特的性质,在数学及生活中有着较广泛的应用。
3) Gauss function


Gauss函数
1.
The number theoretical method is employed to treat problems concerning Gauss function and to seek general ways to solve this kind of problems.
利用数论工具研究涉及Gauss函数的一类问题 ,寻求解决这类问题的一般方法 ,给出了几个一般性定理 ,推广与改进了以往的相关结
2.
With the X-ray tooth image for example, analyzing its characteristics,adopting the Gauss function to construct multiply peak-value curves,and producing matching histogram,is a kind of practical enhancement method.
以牙X线根尖片图像为例,分析图像特征,采用Gauss函数来构造多峰曲线,生成匹配化直方图,是一种实用增强方法。
3.
The extremum drop and the inflexion of Gauss function are distinguished based on the wavelet transformation of Gauss function, and the joining of Gauss function is also distinguished according to the change of wavelet transformation.
利用小波变换能够表征信号特征的特性 ,选取适当小波函数 ,对 Gauss函数作小波变换 ,根据小波变换零值点和极值点来判别 Gauss函数极值点和拐点 ,根据小波变换的变化情况来判别 Gauss函数的重叠情况 。
4) Gauss kernel function


Gauss核函数
1.
Quick algorithm for minimum spheres construction based on Gauss kernel function;


基于Gauss核函数的快速构造最小超球算法
5) Gauss weight function


Gauss权函数
1.
The results of an example indicate that the nonlocal model with the BSpline or Gauss weight function can overcome the problems of both energy and mesh dependence.
通过算例表明,采用B-Spline权函数和Gauss权函数的非局部模型可以较好的避免有限元实现时,计算结果的对网格的依赖性和零能量消耗问题。
6) Gauss integer ring


Gauss整数环
1.
In this paper,we gave the construction of ideal N=(m+ ni) on Gauss integer ring Z[i] and the classify on quotient ring Z[i]/N too.
本文给出了 Gauss整数环 Z[i]的理想 N=(m+ ni)的构造及商环 Z[i]/N的分类。
补充资料:整函数
| 整函数 integral function 在整个复平面上处处解析的函数。整函数总可以在原点 展开成泰勒级数:  ,它在全平面收敛,整函数以∞点为唯一的孤立奇点,它在∞点的罗朗展式与它在原点的泰勒展式有一样的形式。当∞点是整函数的可去奇点时,这个整函数只能是常数,这就是著名的刘维尔定理,通常表述为“有界整函数必为常数”。利用这一定理可以得到代数基本定理的简单证明。当∞点是整函数的n阶极点时,这个整函数是一个n次多项式 ,也就是它的泰勒展式(或罗朗展式)只有有限多项。当∞点是整函数的本性奇点时,这个整函数的泰勒展式一定有无限多项,这类整函数称为超越整函数。由代数基本定理知道n次多项式一定有n个零点(也就是根),它总可以分解为n个一次因式的积,对于超越整函数,它可能有无限多个零点 ,比如sinπz就以全体整数为其零点集,也有的超越整函数没有零点,如ez就处处不为零,一般来说,没有零点的超越整函数总可以表成eg(z)的形式,此处g(z)也是一个整函数,而有无限多个零点的超越整函数f(z)也有一个因子分解式 ;形如 ,它在全平面收敛,整函数以∞点为唯一的孤立奇点,它在∞点的罗朗展式与它在原点的泰勒展式有一样的形式。当∞点是整函数的可去奇点时,这个整函数只能是常数,这就是著名的刘维尔定理,通常表述为“有界整函数必为常数”。利用这一定理可以得到代数基本定理的简单证明。当∞点是整函数的n阶极点时,这个整函数是一个n次多项式 ,也就是它的泰勒展式(或罗朗展式)只有有限多项。当∞点是整函数的本性奇点时,这个整函数的泰勒展式一定有无限多项,这类整函数称为超越整函数。由代数基本定理知道n次多项式一定有n个零点(也就是根),它总可以分解为n个一次因式的积,对于超越整函数,它可能有无限多个零点 ,比如sinπz就以全体整数为其零点集,也有的超越整函数没有零点,如ez就处处不为零,一般来说,没有零点的超越整函数总可以表成eg(z)的形式,此处g(z)也是一个整函数,而有无限多个零点的超越整函数f(z)也有一个因子分解式 ;形如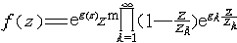 ,其中g(z)是整函数,0是m阶零点,zk是非零零点集,gk( ,其中g(z)是整函数,0是m阶零点,zk是非零零点集,gk( )是 )是 的多项式,这是魏尔斯托拉斯因子分解定理。超越整函数还有一个重要性质:若f(z)是超越整函数,则对任意复数A(包括A=∞),存在点列{zk },使zk 的多项式,这是魏尔斯托拉斯因子分解定理。超越整函数还有一个重要性质:若f(z)是超越整函数,则对任意复数A(包括A=∞),存在点列{zk },使zk  ∞(k ∞(k ∞)而有f(zk) ∞)而有f(zk) A。这一结果有一个更精确的发展:对超越整函数f(z),最多除去一个值(称为例外值)外,对所有其他的复数v值(v≠∞),f(z)-v都有无穷多个零点(毕卡定理)。 A。这一结果有一个更精确的发展:对超越整函数f(z),最多除去一个值(称为例外值)外,对所有其他的复数v值(v≠∞),f(z)-v都有无穷多个零点(毕卡定理)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条