1) the theory of gauge field


规范场论
1.
According to the theory of gauge field,various fundamental interactions in nature are in essence the consequences of gauge field.
根据规范场论,自然界各种不同的基本相互作用在实质上都归结为规范场,而"规范对称性"的本质在于"物理定律在变换中保持内在不变性"。
2) gauge field theory


规范场理论
1.
Based upon Weyl\'s electromagnetic theory,the paper gives a brief review of the construction of non-integrable phase factor and the theory of local gauge transformation in gauge field theory.
介绍了韦耳在规范场理论的建立、发展与完善过程中所作出的重要贡献及规范场中不可积相位因子与定域规范变换理论的建立过程,并简要介绍了规范场作用的两种不同描述方法。
3) the principle of normal field theory


规范场论纲领
4) gauge field theory


[物]规范场理论
5) canonical field theory


规范场论,正则场论
6) From Weyl's Electromagnetic Theory to Gauge Field Theory


韦耳与规范场理论
补充资料:场论
| 场论 fields,theory of 用向量分析研究数学、物理中有关问题的理论。在空间或空间的一部分Ω上分布着某种物理量,就构成一个场。例如物体的密度场、温度场;空间的引力场、流体的速度场等。尽管每种场都有各自的特性,但是在数量关系上各种场都有一定的数学形式,例如温度场是数量场,地球表面的地形可用“海拔”来刻画,这也是数量场,而引力场、速度场是向量场。 设W ?Â3,称函数 u:  为分布在Ω上的一个数量场,而称映射F: 为分布在Ω上的一个数量场,而称映射F: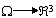 为分布在Ω上的一个向量场。在直角坐标系下,数量场可表为u(P)=u(x,y,z),其中(x,y,z)为P点的坐标,向量场可表为F(P)={F1,F2,F3},其中F1=F1(x,y,z),F2=F2(x,y,z),F3=F3(x,y,z),分别表示向量F(P)在X轴、Y轴和Z轴上的投影,引入坐标系是为了便于运算和进行数学处理,而场本身的性质与坐标系的选取无关。梯度、旋度、散度是场论中的三个基本量。 为分布在Ω上的一个向量场。在直角坐标系下,数量场可表为u(P)=u(x,y,z),其中(x,y,z)为P点的坐标,向量场可表为F(P)={F1,F2,F3},其中F1=F1(x,y,z),F2=F2(x,y,z),F3=F3(x,y,z),分别表示向量F(P)在X轴、Y轴和Z轴上的投影,引入坐标系是为了便于运算和进行数学处理,而场本身的性质与坐标系的选取无关。梯度、旋度、散度是场论中的三个基本量。设在W?Â3上分布着一个数量场u,且对每一P(x,y,z)∈Ω,有连续偏导数 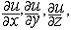 则称向量 则称向量 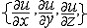 = =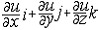 为数量场u在P点的梯度,记作gradu (P)。因此,数量场的梯度是一个向量场,梯度的方向是函数u(P)在P点变化率 最快(或最大)的方向。 为数量场u在P点的梯度,记作gradu (P)。因此,数量场的梯度是一个向量场,梯度的方向是函数u(P)在P点变化率 最快(或最大)的方向。设F=F(P)为向量场,在直角坐标系下,有F(P)={F1(x,y,z),F2(x,y,z),F3(x,y,z)}且 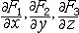 存在、连续,则称函数divF(P)= 存在、连续,则称函数divF(P)=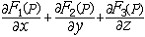 为F 的散度。因此,向量场的散度是一个数量场。假设F(P)是一个流体速度场,则当divF(P)>0时,表示 P 为流出的源,其值表示源的强度,当divF(P)<0时,表示P为吸收的洞,其值表示洞的强度,若divF(P)t=0,则P点既不是源,也不是洞,若在场内取一区域M,其边界 ¶M 为光滑曲面,¶M上任一点的外法线单位向量记为n ,则多元微积分中的高斯公式可表为 为F 的散度。因此,向量场的散度是一个数量场。假设F(P)是一个流体速度场,则当divF(P)>0时,表示 P 为流出的源,其值表示源的强度,当divF(P)<0时,表示P为吸收的洞,其值表示洞的强度,若divF(P)t=0,则P点既不是源,也不是洞,若在场内取一区域M,其边界 ¶M 为光滑曲面,¶M上任一点的外法线单位向量记为n ,则多元微积分中的高斯公式可表为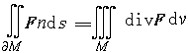
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |