1) categorical proposition
直言命题
1.
This paper carries out full analysis on Aristotle s theory on categorical proposition and points out that he introduced,for the first time in logic history,term variable,established opposition matrix,and laid basis for syllogism.
对亚里士多德的直言命题理论作了全面的分析,指出亚里士多德在逻辑史上第一次引进词项变元,建立了对当方阵,为三段论奠定了基础。
2.
Matching up to the three indispensable conditions to conversion inference of categorical proposition in traditional logic is in fact proved to be the restriction of interrelation between lexical items that the conversion inference concerns, as is visually cleared by Eulerian graph.
直言命题换位推理应当同时满足的三个条件实际上是对此变形推理所涉及的词项关系的制约,欧拉图可以很直观地反映这一点。
3.
Is it universally adequate that the reasoning rule "if a term is not distributive in the premise, it is still not in the conclusion" in the reasoning consisting of categorical propositions? This is a question that has not been resolved in logic.
"在前提中不周延的项,在结论中仍不得周延"这条推理规则在由直言命题组成的推理中是否普遍适用?这是一个在逻辑学中尚未得到解决的问题。
2) classical categorical proposition
传统直言命题
1.
For the classical categorical proposition A, E, I, O as a "propositional form", its logical semantic hasn t been given a clear rule and its logical structure hasn t been shaped completely, so for there exist a variety of problems in logical theory.
传统直言命题A、E、I、O作为“命题形式”其逻辑语义没有规定清楚，逻辑结构尚未完全定型，因而至今还存在种种逻辑理论上的问题。
3) absolute proposition
定言命题; 直言判断
6) disjunctive proposition
选言命题
1.
In our country, logic circles have different views on three theory problems :the definition of compound proposition , the definition of disjunctive proposition and the dignity of exclusive disjunctive proposition.
我国逻辑界对复合命题的定义、选言命题的定义以及不相容选言命题的身份这三个理论问题 ,有不同的观点。
补充资料：直言命题
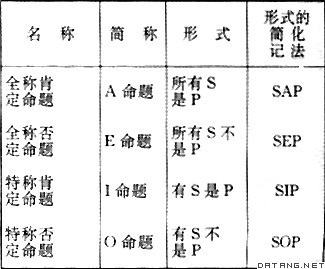
| 直言命题 categorical proposition 直接陈述对象有无某种性质的命题。传统逻辑中的一类最简单的命题。逻辑史上最早详细研究这类命题的是亚里士多德但他并没有使用“直言命题”这个名称，而称之为简单命题。后来I.康德从认识的模态的角度把这类命题叫做实然（原意为断言）命题。传统逻辑学家一般认为，这类命题与选言命题、假言命题不同，它是无条件地、简单地肯定或否定某种事实，因而被汉译为直言命题。 传统逻辑把直言命题分为四种基本类型，即：全称肯定命题、全称否定命题、特称肯定命题和特称否定命题。它们的简称、形式以及形式的简化记法如下：
如果一个直言命题对其主项（或谓项）的全部外延有所反映，那么该主项（或谓项）是周延的；如果一个直言命题没有对其主项（或谓项）的全部外延有所反映，那么该主项（或谓项）是不周延的。根据这一定义，全称命题的主项周延，特称命题的主项不周延。由于“所有S是P”并不意味着所有S是一切P；“有S是P”也不意味着有S是一切P，因之肯定命题的谓项不周延，这是没有例外的。“所有S不是P”，意味着有S不是任何P；“有S不是P”意味着有S不是任何P，因此否定命题的谓项周延 。直言命题中一个词项周延与否，仅与命题形式反映什么有关，它不是主谓项所反映的事物之间的事实上的关系，而是直言命题的含义问题。周延理论是传统逻辑论述换位和三段论有效性的基础。 直言命题中还有一类特殊形式即单称命题。有两种：一种主项是专名，如“苏格拉底是人”；一种主项是附有限制的普遍概念，如“昨天我谈到的那个人是作家”。单称命题有肯定和否定的区别，传统逻辑认为其形式分别为：这个S是P；这个S不是P。亚里士多德虽论及单称命题，但却没有谈到有关单称命题的推理。后来许多传统逻辑读本在论述推理时，把单称命题当作全称命题处理是不妥当的。 现代逻辑克服了传统逻辑不考虑空类和全类，即在S类和P类都既不空又不全的假设下讨论A、E、I、O这四种直言命题的局限。现代逻辑考虑到词项的外延可以是空类和全类，因而全称命题如“凡未接触过细菌的人都不得细菌性传染病”的形式应该为 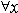 （F(x)→G（x）），这可以读作“对论域里的所有个体x而言，如果x有性质F则x有性质G”；而传统逻辑所谓的特称命题如“有金属是固体”的形式应为（'x（F（x））∧G（x）），这可读作“在论域里至少存在一个体x，使得x有性质F并且x有性质G”。故现代逻辑称这类命题为存在命题。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条