1) p Laplace boundary value problem
p-拉普拉斯方程边值问题
2) p-Laplace equation
p-拉普拉斯方程
1.
The existence of the solution for a singular p-Laplace equation involving critical Sobolev-Hardy exponent is studied: -div〔(|▽u|p-2▽u)/|x|β 〕=(up*-1)/|x|α+λuq-1,inΩ;u=0,onΩ by using Sobolev—Hardy inequality,Concentration Compactness Principle and the Mountain Pass Geometry.
利用Sobolev-Hardy不等式、集中紧原理、山路几何给出关于Sobolev-Hardy指数的含奇性p-拉普拉斯方程:-div〔(|▽u|p-2▽u)/|x|β〕=(up*-1)/|x|α+λuq-1,inΩ;u=0,on
3) singular p-Laplacian equation
奇异p-拉普拉斯方程
4) p(x)-Laplacian equation
p(x)-拉普拉斯方程
5) p(x)-Laplacian
p(x)拉普拉斯方程
6) Generalized p-Laplacian
广义p-拉普拉斯方程
补充资料：拉普拉斯方程
| 拉普拉斯方程 Laplace's equation 以法国P.-S.拉普拉斯命名的二阶偏微分方程。在三维直角坐标系中，它的形式是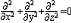：  它的二次连续可微解称为调和函数，调和函数有极多的光滑性。拉普拉斯方程在物理吸广泛应用，因为它的解出现在电、磁、引力位势、稳态温度以及流体动力学各方面的问题中。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条