1) Fraunhofer diffraction field
夫琅禾费衍射场
1.
Fraunhofer diffraction experiment is conducted by using a device that receives diffraction field in a far field condition does, but the result is different from the theoretic values of the Fraunhofer diffraction field.
根据菲涅耳基尔霍夫衍射公式,利用贝塞尔函数的积分表达式得出夫琅禾费衍射场的光强级数解,进而讨论了衍射场的基本特征。
2) Fraunhofer diffraction
夫琅禾费衍射
1.
The diffraction fields at image plane belong to the Fraunhofer diffraction;
像面衍射场系夫琅禾费衍射
2.
A study intensity distribution of the Fraunhofer diffraction field with translation phase factor of the screen;
用衍射屏平移相因子计算夫琅禾费衍射场强分布
3.
Computer simulation of Fraunhofer diffraction experiments;
夫琅禾费衍射的计算机仿真
3) Fraunhofer-diffraction
夫琅禾费衍射
1.
Fraunhofer-diffraction Light Intensity Distribution of the Square Apertures Arranged as Phalanx;
正方形小孔方阵夫琅禾费衍射光强分布
2.
Fraunhofer-diffraction Light Intensity Distribution of the Double Square Holes;
正方形双孔夫琅禾费衍射光强分布
3.
Fraunhofer-Diffraction on a class of figuresconstructed ellipse and rectangle;
一类椭圆与矩形围成图形的夫琅禾费衍射
4) Fraunhofer circular hole diffraction speckle
夫琅禾费圆孔衍射斑
1.
And the approach to a computer simulation on the dynamic superpose of Fraunhofer circular hole diffraction speckles is describe
本文介绍了利用面向对象的程序设计方法实现计算机模拟夫琅禾费圆孔衍射的具体过程 ,给出了用计算机模拟两个夫琅禾费圆孔衍射斑动态叠加过程的具体方
5) Fraunhofer single-slit diffraction
夫琅禾费单缝衍射
6) Fraunhofer
夫琅禾费
1.
On Characteristics of Fraunhofer Matrix Aperture Diffraction and Its Simulation of MATLAB;
夫琅禾费矩孔衍射的特征及其MATLAB模拟
2.
A Study of the Light Intensity Diffracted from Fraunhofer Motion Aperture;
夫琅禾费矩孔衍射的光强
补充资料：夫琅禾费衍射
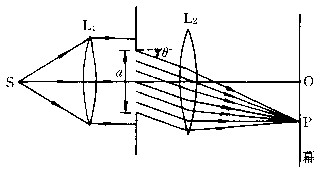
| 夫琅禾费衍射 Fraunhofer diffraction 光源和观察幕离障碍物（孔或屏）均为无穷远的衍射现象。实验装置如图，S为单色点光源，放置在透镜L1的物方焦点处，所得平行光垂直入射到障碍物，借助于透镜L2将无穷远处的衍射图样移至L2的像方焦面上观察。幕上的强度分布可用惠更斯-菲涅耳原理求得。
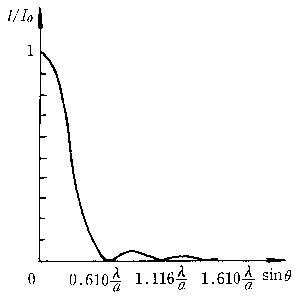
单缝衍射 障碍物为单狭缝，其长度比缝宽a要大得多，故可看作无穷长。由于在缝的长度方向对入射光没有限制，在该方向上不发生衍射；在垂直于缝长方向对光有限制，将发生衍射。幕上P 点的强度I取决于衍射角为θ的衍射光在该点的相干叠加结果，图中为其强度分布曲线 ，I0 为中心点O的光强。θ＝0时，I＝I0，强度达极大值，称衍射主极大（或中央极大）。当衍射角θ满足sinθ＝kλ／a（k＝±1，±2，…，λ为波长)时，I＝0，称衍射极小。相邻两极小间有一次极大，其强度远比中央极大要小，中央极大占有入射能量的绝大部分。 当缝宽a  λ时，所有次极大和极小均向中心点O靠拢，在极限情形下（a→∞ ）缩成一点，此即几何光学的结果。只有当缝宽a与波长λ可比拟时才能观察到明显的衍射现象。衍射极小（或极大）的位置和间距与波长有关，对不同波长的光，除中央极大重合外，其他各级次极大均彼此分离，所以，用白光作为光源时将会得到彩色衍射图样。
圆孔衍射 障碍物为带圆孔的不透光屏。设圆孔半径为a ，幕上将观察到中央为亮斑的同心圆环状衍射图样，其强度分布曲线如图，I0为中央极大中心处(θ＝0)的光强。图中一系列极小值对应暗圆环，相邻两极小间的次极大对应亮圆环。中央亮斑称为爱里斑，约占入射能量的84％。小角衍射时爱里斑的半角宽为 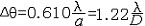 D为圆孔直径。D愈大，爱里斑的直径愈小，各级次极大均向中心靠拢，D>>λ 时，整个衍射图样缩成中心的一个点，此即几何光学的结果。
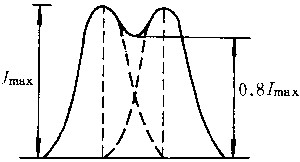
光学成像仪器中的透镜均有圆形边框，望远镜的物镜将产生夫琅禾费圆孔衍射，这使所成像不是由几何光学的像点而由一系列爱里斑组成，这必然影响像的清晰度。两个离得很近的爱里斑刚能分辨的标准是由J.W.S.瑞利提出，称瑞利判据。瑞利判据为：两强度分布相同的爱里斑重叠后，其总光强分布曲线中央凹陷处的光强为最大光强的80％时刚好能分辨。此情形相当于一个亮斑的第一极小恰好与另一亮斑的中央极大重合（见图）。能分辨出两个亮斑的最小角间距称为最小分辨角，它等于 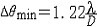 可用物镜的最小分辨角来表示它的分辨本领。直径D愈大，分辨本领就愈高，这就是为什么天文望远镜的直径设计得越来越大的原因之一。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条