1) Fraunhofer diffraction
夫朗禾费衍射
1.
Based on the Fraunhofer diffraction theory and a microlens,a high-performance complex optical system for a digital sun sensor is designed.
以夫朗禾费衍射理论为基础,结合微透镜,设计了一种高性能的数字式太阳敏感器复合光学系统。
2) Fraunhofer diffraction
夫琅禾费衍射
1.
The diffraction fields at image plane belong to the Fraunhofer diffraction;
像面衍射场系夫琅禾费衍射
2.
A study intensity distribution of the Fraunhofer diffraction field with translation phase factor of the screen;
用衍射屏平移相因子计算夫琅禾费衍射场强分布
3.
Computer simulation of Fraunhofer diffraction experiments;
夫琅禾费衍射的计算机仿真
3) Fraunhofer-diffraction
夫琅禾费衍射
1.
Fraunhofer-diffraction Light Intensity Distribution of the Square Apertures Arranged as Phalanx;
正方形小孔方阵夫琅禾费衍射光强分布
2.
Fraunhofer-diffraction Light Intensity Distribution of the Double Square Holes;
正方形双孔夫琅禾费衍射光强分布
3.
Fraunhofer-Diffraction on a class of figuresconstructed ellipse and rectangle;
一类椭圆与矩形围成图形的夫琅禾费衍射
4) Fraunhofer diffraction field
夫琅禾费衍射场
1.
Fraunhofer diffraction experiment is conducted by using a device that receives diffraction field in a far field condition does, but the result is different from the theoretic values of the Fraunhofer diffraction field.
根据菲涅耳基尔霍夫衍射公式,利用贝塞尔函数的积分表达式得出夫琅禾费衍射场的光强级数解,进而讨论了衍射场的基本特征。
5) fraunhofer diffraction
夫朗和费衍射
1.
The difference of Fraunhofer diffraction between Information Optics and Physical Optics is analysed, the consistence of which is pointed out about one single object.
分析信息光学和物理光学中夫朗和费衍射的差别 ,指出在研究单个物体的夫朗和费衍射二者的一致性 ,根据普适的夫朗和费衍射的定义 ,导出夫朗和费衍射的近似条件。
2.
It is pointed out that the methods of the approximate treatment of the Fraunhofer diffraction under spherical wave illumination in literatures [1-7] are not very proper.
本文认为文献[1]～[7]对球面波照明下的夫朗和费衍射的若干近似处理方法不是十分妥当的。
3.
The analysis of the Fraunhofer diffraction pattern of the twin rectangle aperture;
利用Mathematica软件 ,通过夫朗和费衍射公式计算双矩孔的衍射光强 ,并且绘制出了衍射图样 。
6) Fraunhofer diffraction
夫朗荷费衍射
1.
Error research in measuring small dimensions by Fraunhofer diffraction;
微小尺寸夫朗荷费衍射测量中的误差研究
补充资料：费多罗夫，..
Feiduoluofu
费多罗夫，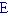
.
.
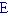
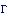
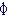
(1853～1919)
[]
俄国岩石学家和矿物学家，结构晶体学家。1853年2月22日生于奥廉堡,1919年5月21日卒于彼得格勒
1872年毕业于军事工程学校。1883年毕业于圣彼得堡矿业学院。曾任乌拉尔图林斯克矿区矿业工程师，莫斯科农学院教授，圣彼得堡科学院副院长，圣彼得堡矿业学院院长。1896年当选为巴瓦尔斯克科学院院士，1919年当选为俄罗斯科学院院士。1885年费多罗夫完成《图形学基础》,其中提出的平行面体学说,成为研究晶体结构理论的基础。1890年他在《等轴晶系对称》中首次推导出晶体结构对称可能有的形式，即230个空间群,并且发现了结晶学极限定律，为晶体化学的诞生奠定了基础。1889年，他发明了双圈反射测角仪，方便了晶体测角的工作。1891年,又发明万能旋转台(或称费氏旋转台),可以在不同方向上对作光学性质的研究。他还提出用“费氏化学四面体”图示法来表示某些和复杂的化学成分。主要著作还有《结晶学教程》(1891,1897,1901)和《晶体的对称和结构论文精选》(1949)等。
王根元 赵福堂
费多罗夫，
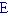
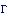
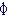
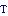
.. (1853～1919)[]
俄国岩石学家和矿物学家，结构晶体学家。1853年2月22日生于奥廉堡,1919年5月21日卒于彼得格勒1872年毕业于军事工程学校。1883年毕业于圣彼得堡矿业学院。曾任乌拉尔图林斯克矿区矿业工程师，莫斯科农学院教授，圣彼得堡科学院副院长，圣彼得堡矿业学院院长。1896年当选为巴瓦尔斯克科学院院士，1919年当选为俄罗斯科学院院士。1885年费多罗夫完成《图形学基础》,其中提出的平行面体学说,成为研究晶体结构理论的基础。1890年他在《等轴晶系对称》中首次推导出晶体结构对称可能有的形式，即230个空间群,并且发现了结晶学极限定律，为晶体化学的诞生奠定了基础。1889年，他发明了双圈反射测角仪，方便了晶体测角的工作。1891年,又发明万能旋转台(或称费氏旋转台),可以在不同方向上对作光学性质的研究。他还提出用“费氏化学四面体”图示法来表示某些和复杂的化学成分。主要著作还有《结晶学教程》(1891,1897,1901)和《晶体的对称和结构论文精选》(1949)等。王根元 赵福堂
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条