1) Parabolo-hyperbolic mixed type


双曲抛物混合型
2) parabolo-hyperbolic mixed equation


抛物双曲混合型方程
1.
Using the D Alembert formula and the Fourier method, the solution of the moving boundary problem for the nonhomogeneous parabolo-hyperbolic mixed equation of the second order is obtained in this paper.
本文运用D’Alembert公式和Fourier方法,求出了一类非齐以二阶抛物双曲混合型方程移动边界问题的解。
2.
using the Riemann method and the Fourier method,this paper discusses a class of boundary problems for the parabolo-hyperbolic mixed equation of second order with a moving boundary.
利用Riemann方法和Fourier方法讨论了二阶抛物双曲混合型方程带有移动边界的一类边值问题。
3.
This paper studies the boundary problem for the parabolo-hyperbolic mixed equationof third orderunder the boundary conditions:It is proved in this paper that the problem is correct if and only if a≠0.
本文研究三阶抛物双曲混合型方程带有边界条件的边值问题。
3) hyperbolic-parabolic equation


双曲-抛物型方程
1.
The singularly perturbed generalized initial-boundary value problem for the hyperbolic-parabolic equation is considered.
讨论了一类奇摄动双曲-抛物型方程广义初边值问题,在适当的条件下,用Galerkin方法研究了广义解的存在性、唯一性,同时得到了解的渐近估计式。
4) Parabolic-hyperbolic equation


抛物双曲模型
5) parablic-hyperbolic system


抛物-双曲耦合组
6) parabolic variable-thickness double-curved arch dam


抛物线型变厚双曲拱坝
1.
CAD is used to perform the calculating and drawing jobs of the parabolic variable-thickness double-curved arch dam of Nanzhang Xiakou hydropower project, such as the calculation of the arc length and the thickness and area of the arch rings, the volume of the dam etc.
针对抛物线型变厚双曲拱坝 ,用计算机辅助设计解决了弧长、面积、体积、坐标、任意空间平面和 2种扭面的横剖面图、平面拱圈图、展开或不展开立视图、扭面分缝线图、牛腿或廊道斜底面与坝体的交点等的计算和绘图工作。
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 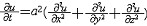 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式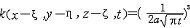 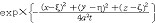 热传导方程初值问题的解可用基本解叠加而成,即 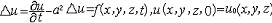 的解为 的解为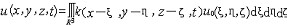 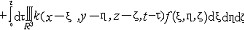 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 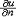 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条