1) Multi fractal dimension spectrum
多重分形维数谱
2) multifractional spectrum parameter
多重分形谱参数
3) multifractal dimensions
多重分形维数
1.
The paper is based on the idea of combining fractal theory with information theory to establish a correspondence between multifractal dimensions of chaos game representation of proteins and Rényi entropy rate of symbolic sequences via probabilistic measure μ.
文中将分形理论与信息论方法相结合,把蛋白质混沌游走表示法的多重分形维数和符号序列的Rényi熵率之间通过概率测度μ建立对应关系,从而使蛋白质序列的研究转为符号序列的可视化分析,在生物信息学上具有一定的应用前景。
4) multifractal spectrum
多重分形谱
1.
Application of multifractal spectrum in leaf images processing;
多重分形谱在叶片图像处理中的应用
2.
Study on multifractal spectrum of LAN traffic and their correlations;
局域网流量的多重分形谱分析及关联性研究
3.
Multifractal dimension and multifractal spectrum algorithm based on Z-ordering technique
基于Z-ordering的多重分形维数及多重分形谱算法
5) multi-fractal spectrum
多重分形谱
1.
We propose to analyze the TEM image firstly,then,we quantitatively their structural topography of microscope image of semi-continuous Ag films with multi-fractal spectrum.
对TEM显微图像,提出了利用小波变换消除显微图像中的低阶趋势项,然后用多重分形谱来定量表征不同厚度半连续Ag膜的复杂微结构特征。
2.
A new method for diagnosing single phase-to-earth faultsis presented, which is based on multi-fractal spectrum calculated bycomputer emulator.
然后运用MATLAB进行仿真计算,得到线路零序电流的多重分形谱,提出了利用多重分形谱对线路的零序电流进行分析,根据谱图进行判断故障线路的新方法。
3.
The multi-fractal spectrum which is used to deal with the discontinuous, weak and non-stationary fault signals can well analysis the process about the neutral un-direct grounding.
利用能够对突变的、微弱的非平稳的故障信号进行处理的多重分形谱分析,可以很好的分析小电流接地系统单相接地故障暂态过程并提取故障特征,所以本文利用多重分形与小波变换相结合进行故障选线的研究,更好地解决了小电流接地系统单相接地故障的选线问题。
6) multifractal spectra
多重分形谱
1.
In this paper,the dimension and multifractal spectra of diffusion aggregation cluster with next-nearest neighbor are obtained by computer simulation.
通过计算机仿真模拟,研究了次近邻扩散聚集集团的维数与多重分形谱。
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 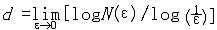 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条