1) multifractal
多重分形维
1.
Analysis of multifractal based on FA singular measurement
基于FA奇异测度的多重分形维分析
2) multifractal dimensions
多重分形维数
1.
The paper is based on the idea of combining fractal theory with information theory to establish a correspondence between multifractal dimensions of chaos game representation of proteins and Rényi entropy rate of symbolic sequences via probabilistic measure μ.
文中将分形理论与信息论方法相结合,把蛋白质混沌游走表示法的多重分形维数和符号序列的Rényi熵率之间通过概率测度μ建立对应关系,从而使蛋白质序列的研究转为符号序列的可视化分析,在生物信息学上具有一定的应用前景。
3) Multi fractal dimension spectrum
多重分形维数谱
4) multifractal dimension
多重分维
1.
The damage tensor, filled fractal dimension and multifractal dimension values of jointed rock mass of each measuring points in the tunnel are computed in Jiefanggou dam,Jinping hydroelectric power station.
计算了锦屏水电站解放沟坝段平硐测点节理岩体的损伤张量、充填维数及多重分维值；建立了充填维数与连通率、多重分维值与最大主损伤值的关系式，初步明确了分维的物理意义，并对其可能的应用作了分析。
2.
Relationships between statistical physics and message entropy,between message entropy and message dimension,between generalized entropy function and multifractal dimension are indicated,and accordinglysome physical foundations for message theory and its foremost application are given.
阐明了统计物理熵与信息熵 ,信息熵与信息维的联系 ,以及广义熵函数与多重分维的联系 ,从而给信息论及其前沿应用提供了物理学依
5) Multifractal
多维分形
1.
Spatial distribution of soil Pb in Tongling areas based on multifractal method;
基于多维分形的铜陵地区土壤中Pb元素空间分布
2.
The study of metallogenic anomaly identification based on deep soil data with multifractal method——A case study of Cu element in Tongling ore clustering area
基于深层土壤数据的多维分形成矿异常识别研究——以铜陵矿集区Cu元素为例
6) multifractal
多重分形
1.
Application of multifractal to ore-forming potential evaluation;
多重分形方法在金属成矿潜力评价中的应用
2.
Multifractal Analysis of Genomes Sequences CGR Graph;
基因组序列CGR图形表示的多重分形分析
3.
Mmultifractal analysis of intestinal pressure data;
结肠道压力数据的多重分形分析
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 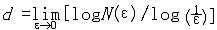 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条