1) probabilistic quasi-metric family space
概率准度量族空间
1.
in this paper, we introduce the concepts of quasi-metric family spaces with an index set, and discuss the relationship between quasi-metric family spaces with an index set, probabilistic quasi-metric family spaces and random quasi-metric family spaces.
引入了带指标的准度量族空间的概念，讨论了带指标的准度族空间与概率准度量族空间和随机准度量族空间之间的关系，建立了这些空间的一些性质，研究了这些空间的等矩同构。
2.
In this paper, we introduce the concepts of probabilistic quasi-metric family spaces,probabilistic quasi-norm family spaces, spandom quasi-metric family spaces and random quasi-normfamily spaces.
引入了概率准度量族空间、概率准范数族空间、随机准度量族空间和随机准范数族空间的概念，包括了现有的各种相关空间类[1～11]（特别是[8，9]）作为特殊情况，建立了统一的空间体系。
2) quasi-metric family space with an index set
准度量族空间
3) probabilistic metric space
概率度量空间
1.
The main result in the reference is improved with a great reduction of its proof procedure,and a probabilistic metric space is proposed that finds important applications in probabilistically differential equation theory.
把文献[1]中的引理推广为分析概率论中有用的极限定理,改进了文献[1]的主要结果及简化了其证明过程,并获得了一个在概率微分方程理论中有重要应用的实用概率度量空间；给出了随机线性泛函延拓定理的应用；建立了概率微分方程解的局部存在性定理。
2.
Paper,partial order is introduced in probabilistic metric space.
利用泛函在概率度量空间中引入半序,并利用此半序的方法研究了概率度量空间中的非线性算子方程Lx=Ax的可解性问题,得到了几个新的定理,同时推广了若干重要定理。
3.
These results not only unify and extend the corresponding results of usual metric spaces and Menger probabilistic metric spaces,but also cont.
这些定理不仅推广与统一了通常度量空间与Menger概率度量空间的相应结果,而且也包含了Kaleva-Seikkala模糊度量空间中压缩型映射的不动点定理作为其特殊情形。
4) Menger probabilistic metric space
Menger概率度量空间
1.
This dissertation deals with some new fixed point theorems in Menger probabilistic metric spaces, which include common fixed point theorems of weakly compatible mappings under strict contractive conditions and common fixed point theorems of compatible and weakly compatible mappings underφ-contractive conditions.
本文研究Menger概率度量空间中某些新的不动点定理，主要包括严格压缩条件下的弱相容映射的公共不动点定理和φ-压缩条件下的相容和弱相容映射的公共不动点定理。
5) probabilistic n-metric space
概率n-度量空间
6) generating space of quasi_metric family
准度量族生成空间
1.
The first is that a PM space (E,F) is isometrically isomorphic to another PM space (E′,F′), and the second is that a PM space (E,F) is isometrically isomorphic to a generating space of quasi_metric family (E′,d r,r∈(0,1)).
概率度量空间理论中有两种等距同构 ,一种是一个概率度量空间等距同构于另一个概率度量空间· 另一种是一个概率度量空间等距同于一个准度量族生成空间· 该文建立了这两种等距同构之间的联系
补充资料：度量空间
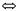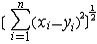| 度量空间 metric space 具有度量的抽象空间，设X是一个集合，若有定义在X×X上的非负实值函数d，满足①d（x，y）≥0，d（x，y）＝0  x＝y； ②d（x，y）＝d（y，x）；③d（x，z）≤d（x，y）＋d（y，z），则称（X，d）是度量空间，d称为距离或度量。这是最接近于欧几里得空间的抽象空间。利用度量可很自然地将欧几里得空间上点的邻域、开集、闭集，收敛序列以及连续映射等概念推广到一般度量空间，也能将一致连续的概念推广到度量空间。由于19世纪末集合论产生后，实变函数及泛函分析的发展，需要规定函数间的距离，因而抽象出度量、度量空间的概念，其创始人是M.R.弗雷歇。常见的度量空间有：n维欧几里得空间（Rn,d）：Rn＝｛（x1，…，xn）｜xi∈R，i＝1，2，…，n ｝，d（x，y）＝  ，其中x＝（x1，x2，…， xn），y＝（y1，y2，…，yn）。希尔 伯特空 间（l2；d）：l2＝｛（x1，x2，…，xn…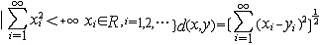）  ， 其中x ＝( x1，x2 ，…），y＝（y1，y2，…）∈l2。函数空间(ρ[0，1］，d)：C[0，1］＝｛f：f为[0，1］上的实值连续函数｝，对任意f，g∈C[0，1］，d(f，g)＝max｛｜f（x）－g（x）｜｝。 x∈[0，1］ 对度量空间（X，d）可引进拓扑结构，即以包含开球B（x，r）＝｛y∈X｜d（ x，y）＜r ｝的集为邻域定义拓扑，称为d所诱导的拓扑。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条