1) minimal conical surface


极小锥面
2) strong minimal cone


强极小锥
1.
By means of the characteristics of strong minimal cone, some existence theorems for solutions are obtained.
考虑了Banach空间中形如x(t) =u(t) + ∫Gtf(t,s,x(s) )ds的广义Volterra积分方程 ,并利用强极小锥的性质 ,获得了以上方程的解的某些存在性结果 。
2.
In this paper,by using the character of strong minimal cone ,we obtain existence theorems of solutions for the nonlinear functional boundary value problem as following:x (n) -∑A i(t)x (i-1) =f(t,x,x′,.
利用“强极小锥”的概念 ,获得了Banach空间中的形如“x(n) - ∑Ai(t)x(i- 1) =f(t,x ,x′,… ,x(n- 1) ) (0 ≤t≤ 1) ,B(x ,x′,… ,x(n- 1) ) =θ”的非线性泛函边值问题的解的存在性结果 。
3.
Abstract In this paper, by using the character of strong minimal cone, we obtain existencetheorems of global solutions for the nonlinear impulsive Volterra integral equations in Banachspaces, that improve the corresponding results presented in [1-3].
本文利用“强极小锥”的概念,获得了Banach空间中非线性脉冲Volterra型积分方程整体解的存在性定理,改进了现有文献中的某些结果。
3) minimal cone


极小锥
4) T monotone increasing operator


全序极小锥
5) Cone-Super minimum solution


锥-超极小解
6) minimal surface


极小曲面
1.
Mius minimal surface in sphereS~n(1);


球面S~n(1)中的Mius极小曲面
2.
About the general parametric solutions for minimal surface equations;


关于极小曲面方程的参数通解
3.
Fairing Minimal Surface by 4-Point Interpolation Subdivision Scheme;


利用四点插值细分法构造光顺极小曲面
补充资料:锥面
| 锥面 conical surface 动直线经过一定点且保持与定曲线相交所产生的曲面。定点称为锥面的顶点;定曲线称为锥面的准线;动直线称为锥面的直母线。当准线是圆时所得锥面称为圆锥面,特别地,如果顶点在过圆心且与圆所在平面垂直的直线上,所得锥面称为直圆锥面(或正圆锥面)。直圆锥面也可以看成是过定直线g上一定点O且与该定直线保持定角a(锐角)的动直线产生的,定点O是它的顶点,定直线g是它的轴,定锐角a是它的半顶角。一般地,以平面上的椭圆、双曲线和抛物线为准线,平面外一点为顶点的锥面,称为二次锥面,它的标准方程为 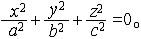
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |