1) molecular orbital theoretical calculation


分子轨道理论计算
2) AM1 molecular orbital theory calculation


AM1分子轨道理论计算
3) Hückel molecule orbital calcultion


休克尔分子轨道理论计算
4) RHF MO calculation


RHF分子轨道计算
5) MNDO molecular orbital calculations


MNDO分子轨道计算
6) Molecular Orbital Calculation


分子轨道计算
补充资料:分子轨道理论
| 分子轨道理论 molecular orbital theory 一种化学键理论。原子轨道理论对分子的自然推广。其基本观点是:物理上存在单个电子的自身,只受分子中的原子核和其他电子平均场的作用,以及泡利不相容原理的制约;数学上则企图将难解的多电子运动方程简化为单电子方程处理。因此,分子轨道理论是一种以单电子近似为基础的化学键理论。描写单电子行为的波函数称轨道(或轨函),所对应的单电子能量称能级。对任何分子,如果求得了它的系列分子轨道和能级,就可以像讨论原子结构那样讨论分子结构,并联系到分子性质的系统解释。有时,即便根据粗糙的计算方案所得到的部分近似分子轨道和能级,也能分析出很有用处的定性结果。 正如在原子轨道理论中,氢原子的严格解提供了进一步发展的理论模式,氢分子离子 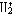 中,单个电子在固定核间距R 的双质子场中的波动 方程解,即氢分子离子的分子轨道是分子轨道理论进程中的基石。 中,单个电子在固定核间距R 的双质子场中的波动 方程解,即氢分子离子的分子轨道是分子轨道理论进程中的基石。  的分子轨道用符号σ、π、δ、…表征,对应于精 确解中的 量子数m=0,±1,±2 ,…,它描述相对于核间距R的轨道对称行为。此外,还需用g和u表征相对于分子中心反演的对称行为。综合起来, 的分子轨道用符号σ、π、δ、…表征,对应于精 确解中的 量子数m=0,±1,±2 ,…,它描述相对于核间距R的轨道对称行为。此外,还需用g和u表征相对于分子中心反演的对称行为。综合起来,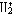 的分子轨道用σg 、σu、πg 、πu 、…等符号表征 ,借助精确求解固定核间距R 的波动方程获 得。其中两个能量最低的轨道为1σg和1σu,在能量E随R的变化曲线中,1σg能级有一极小值( R=2a0,a0 为玻尔半径),代表基态。1σu的行为不同 ,能量随R减 少而单调 上升,显示排斥态的本质。1σg和1σu也被称作成键轨道和反键轨道。作为一种近似处理 ,分子轨道可以当作原子轨道的线性组合 ,简写为LCAO,它的一般形式是: 的分子轨道用σg 、σu、πg 、πu 、…等符号表征 ,借助精确求解固定核间距R 的波动方程获 得。其中两个能量最低的轨道为1σg和1σu,在能量E随R的变化曲线中,1σg能级有一极小值( R=2a0,a0 为玻尔半径),代表基态。1σu的行为不同 ,能量随R减 少而单调 上升,显示排斥态的本质。1σg和1σu也被称作成键轨道和反键轨道。作为一种近似处理 ,分子轨道可以当作原子轨道的线性组合 ,简写为LCAO,它的一般形式是: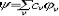 。式中ψ是分子轨道或轨函; 。式中ψ是分子轨道或轨函;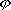 υ是属于各组成原子的原子轨道;cυ 是待定系数 ,由变分法确定。 υ是属于各组成原子的原子轨道;cυ 是待定系数 ,由变分法确定。用 LCAO近似来讨论任意双原子分子中,分属两个原子a和b的一对原子轨道 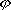 a和 a和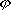 b( 能量分别为 Ea和Eb )形成分子轨道的最优条件,得到有效的成键作用决定于 3 个条件:①能量近似条件,即│Ea-Eb│愈小愈好。②最大重叠条件,即 b( 能量分别为 Ea和Eb )形成分子轨道的最优条件,得到有效的成键作用决定于 3 个条件:①能量近似条件,即│Ea-Eb│愈小愈好。②最大重叠条件,即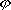 a和 a和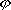 b的重叠愈大,成键作用可能愈大。③对称性条件。 b的重叠愈大,成键作用可能愈大。③对称性条件。可将上述概念和方法推广用于复杂的多原子分子,但不能精确求解,利用对称性分析(群论),可建立能级相关图、分子轨道对称守恒原理和休克分子轨道法等。进一步考虑电子间的排斥作用,建立了哈特里 - 福克方程自洽场分子轨道法以及多种组态相互作用分子轨道从头计算方法。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条