1) generalized dimension
广义分形维数
1.
The self-similar generalized dimensions D(q) and multifractal spectrum are carried out.
对正负电子对撞中Z0衰变能区产生的末态粒子系统的Levy稳定性问题进行了研究,计算出了Levy稳定性指数,得到了该系统自相似的广义分形维数和广义分形谱函数。
2) generalized fractal dimension
广义分数维
1.
The generalized fractal dimension model of tunnel perimeter in jointed rock mass is put forward;and the relation between affecting parameters and generalized fractal dimension of tunnel perimeter is s.
影响隧洞围岩超挖的主要因素是岩体的地质特征和地质组成,对岩体在开挖过程中会遇到超挖问题,将从岩石的破坏机理出发,研究裂隙岩体开挖后的隧洞周边分数维,并提出了裂隙岩体隧洞开挖周边的广义分数维模型。
3) general dimension
广义维数
1.
Aiming at that the reciprocating compressor vibration signals are nonlinear and non-stationary,multifractal spectrum and general dimension are applied to analyze compressor vibration signals and extract fault feature which can be identified.
针对往复压缩机振动信号的非线性和非平稳性,使用多重分形谱和广义维数对压缩机振动信号进行分析,从中提取可识别的故障特征。
2.
The multi-fractals theory is applied for proposing the calculation formula of general dimension least square method.
运用多重分形理论,提出广义维数最小二乘法的计算公式,对实测的时域信号进行了广义维数计算,得到广义维数序列值,并从广义维数中获取盒维数、信息维数、关联维数以及敏感维数。
3.
The multifractal features are extracted from the vibration signals of different spots on reciprocating compressor using the improving arithmetic,the general dimension spectrum of bearing .
采用多重分形改进算法提取往复压缩机振动信号的多重分形特征,得到了轴承故障的广义维数谱。
4) generalized dimension
广义维数
1.
The generalized dimension and sensitive dimension of the vibration mode and displacement for the crack disk were calculated and analyzed by using multi-fractal theory.
运用有限元方法对裂纹圆盘进行了动态分析,获得了其振型和位移响应;应用多重分形理论计算和分析了裂纹圆盘的振型、位移响应的广义维数和敏感维数,把广义分形维数、敏感维数作为裂纹圆盘故障的特征量,对裂纹圆盘的裂纹诊断与识别进行了定性及定量研究;针对裂纹圆盘的振型、位移响应的广义维数,提出在局部范围内,用局部线性法对圆盘裂纹长度进行定量识别,得到了定量识别裂纹长度的计算公式,通过实例计算考查了裂纹长度的计算精度。
2.
Multi-fractal generalized dimension is put forward.
针对传统的分形维数作为图像纹理特征表示时缺少图像分布特征的不足,引入了多重分形的概念和广义维数,并对原图像和灰度差分图像重新提取了图像的纹理特征。
3.
The relevant properties of generalized dimension D q , mass index τ(q) , singularity α(q) and singularity spectrum f(α(q)) are derived rigorously, which are somewhat similar to those obtained from multifractals defined via Renyi information but more general in m.
研究了用配分函数法定义的多重分形理论中奇异谱的几何特性 ,通过严格的数学推理证明了广义维数 Dq、质量指数 τ( q)、奇异性指数 α( q)和奇异谱 f( α( q) )的有关性质 ,明确提出了判定合理奇异谱 f( α( q) )的准则 ,给出了在参数 q→±∞时计算相应函数极限的解析算法。
5) generalized dimensions
广义维数
1.
In bimodal maps, there is a global regularity between the generalized dimensions D q(Z) and scaling factors ｛α C(Z),α D(Z)｝ for q>-1:D q(Z) log |Z| |α C(Z)α D(Z)|=β (2) q,which is independent of symbolic sequences Z ;when q ≤-1,this global regularity is broken.
在双峰映射中 ,当 q >- 1,Feigenbaum型吸引子的广义维数Dq(Z)与标度因子 {αC(Z) ,αD(Z) }之间 ,存在着一个不依赖于符号序列Z的整体规律 :Dq(Z)log｜Z｜｜αC(Z)αD(Z) ｜ =β(2 )q ;当 q≤ - 1,该整体规律遭到破坏 。
2.
The generalized dimensions Dq,q= 2 - 5,are calculated.
计算了广义维数Ｄｑ（ｑ＝２－５），并与由标度阶乘矩方法得到的结果作了比较。
6) generalized fractal
广义分维
1.
The application of generalized fractal in arrival time detection of seismograms;
广义分维在地震信号初至检测中的应用
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 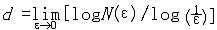 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条