1) Gamma distribution with three parameters


三参数伽玛分布
1.
In this paper,the research on the parameter estimation of Gamma distribution with three parameters and the test of the location parameters has been made.
该文考虑了混合分布为三参数伽玛分布时的参数估计以及位置参数的检验问题。
2) log gamma distribution


对数伽玛分布
1.
The author expands the regeneration of the lognormal distribution to the log gamma and negative log gamma distribution.
本文研究了随机利率的再生性问题 ,把对数正态分布具有的再生性扩展到对数伽玛分布和负对数伽玛分布上 ,同时还得到其它一些与再生性、准再生性相关的结果 。
3) Gamma-function distribution


伽玛函数分布
4) negative loggamma distribution


负对数伽玛分布
1.
X reconciles loggamma distribution or negative loggamma distribution for α and λ.


设X服从以α和λ为参数的对数伽玛分布或负对数伽玛分布,V服从以β为参数的负幂分布,则在X
5) Gamma distribution


伽玛分布
1.
The operational availability of a K/n system with the maintenance time submitted to gamma distribution under(n,r,r) maintenance strategy;
维修时间服从伽玛分布的K/n系统在(n,r,r)维修策略下的可用度
2.
More life distributions, Gamma distribution,and reliability characteristic are discused in this paper.
目前所有文献研究的都是部件寿命服从指数分布时的情况,本文将等效因子的概念推广到常见的伽玛分布。
3.
The paper studies the auto-covariance estimation of Gamma distribution by using the asymptotic behavior of student U -statistic,gives the large sample interval estimation for the scale parameter,and carries out the computing simulation according to the method of random simulation.
利用学生氏U-统计量的渐近性质,研究伽玛分布的自协方差估计,同时给出了尺度参数的大样本区间估计,并采用随机模拟的方法进行计算模拟。
6) negative gamma distribution


负伽玛分布
1.
Using the definition of the maximal Pearson-χ2 distance,the Pearson-χ2 distance of gamma distribution and negative gamma distribution,and its asymptotic properties are discussed.
利用Pearson-χ2最大距离的定义,探讨了伽玛分布类和负伽玛分布的Pearson-χ2最大距离及其渐近性。
补充资料:分布参数电路
| 分布参数电路 distributed parameter circuit 必须考虑电路元件参数的分布性的电路。参数的分布性指电路中同一瞬间相邻两点的电位和电流都不相同,即电路中电压和电流不仅是时间的函数,还是空间坐标的函数。 判别电路是否为分布参数电路,取决于电路本身的最大线尺寸 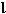 和电路内电流或电压波长λ间的关系。当λ 和电路内电流或电压波长λ间的关系。当λ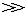 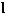 时 ,电路可视为集总参数电路;否则,需看作分布参数电路。电力系统中,远距离的高压电力传输线即是典型的分布参数电路 ,因50赫的电流、电压其波长虽为6000千米,但线路长度达几百甚至几千千米,已可与波长相比。通信系统中发射天线等的实际尺寸虽不太长,但发射信号频率高、波长短 ,也应作分布参数电路处理。 时 ,电路可视为集总参数电路;否则,需看作分布参数电路。电力系统中,远距离的高压电力传输线即是典型的分布参数电路 ,因50赫的电流、电压其波长虽为6000千米,但线路长度达几百甚至几千千米,已可与波长相比。通信系统中发射天线等的实际尺寸虽不太长,但发射信号频率高、波长短 ,也应作分布参数电路处理。传输线方程 将均匀传输线(参数沿线均匀分布的二线传输线)分成许多长度元dx,对该长度元忽略参数的分布性可得出其集总参数电路模型。将每个长度元都这样处理后 ,得出的由许多集总参数电路作为环节级联而成的链形电路就是整个均匀传输线的电路模型,对此长度元的集总参数电路模型可用基尔霍夫定律导出偏微分方程组 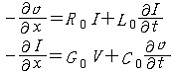 这方程组称为传输线方程,其另一形式为 这方程组称为传输线方程,其另一形式为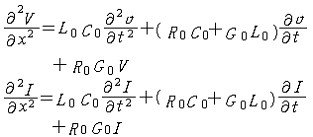 这方程组即为亥维赛电报方程。其中V、I为传输线某点的瞬时电压和电流;R0代表单位长度线(包括来线与回线)的电阻,L0代表单位长度来线与回线的电感,C0和G0分别代表单位长度来线与回线间的电容和漏电导,这些参数称为原参数,其值由导线所用材料、截面的几何形状和尺寸、导线间的距离以及导线周围介质决定。 这方程组即为亥维赛电报方程。其中V、I为传输线某点的瞬时电压和电流;R0代表单位长度线(包括来线与回线)的电阻,L0代表单位长度来线与回线的电感,C0和G0分别代表单位长度来线与回线间的电容和漏电导,这些参数称为原参数,其值由导线所用材料、截面的几何形状和尺寸、导线间的距离以及导线周围介质决定。行波、入射波和反射波 长线的电压和电流正弦稳态解中的两个分量的波形皆随时间的变化而沿 x 线移动,称为行波。沿线从始端向终端传播的行波称为入射波,从终端向始端传播的行波称为反射波。它们的振幅皆按因子 e-βx决定的指数律衰减,β称衰减系数。 无损耗传输线 原参数中代表耗能的参数R0=0和C0=0的均匀传输线。又称无损长线。高频传输线可近似按无损耗传输线处理。这种线的特性阻抗是纯电阻,其电压与电流同相,所以行波的波速与频率无关。无损耗传输线在空载时,电压和电流成为驻波。在 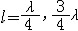 ,…时入端阻抗为零,相当于电压谐振;在 ,…时入端阻抗为零,相当于电压谐振;在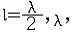 …时,入端阻抗无限大,相当于电流谐振。入端阻抗的上述性质使得无损耗传输线在高频电路中获得多方面的应用。 …时,入端阻抗无限大,相当于电流谐振。入端阻抗的上述性质使得无损耗传输线在高频电路中获得多方面的应用。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条