1) transcendental entire solution


超越整函数解
2) transcendental entire function


超越整函数
1.
This paper analyzes the dynamic properties of semigroups generated by a family of transcendental entire functions with the semigroup operation being functional composition.
考察了由一族超越整函数生成的半群的的动力学性质,其中半群运算是函数的复合。
2.
In this paper,we obtained the following results:Let f was a transcendental entire function with log M(r,f)=O*(e(log r)α)(0≤α<1)(i.
作者得到下列结果:设f是超越整函数,且logM(r,f)=O*(e(logr)α)(即存在两个正实数K1,K2,使得K1≤logM(r,f)/e(logr)α≤K2,其中0<α<1)。
3.
It is proven that compound function φ(z)=f{g(z)} of finite positive order transcendental meromorphic function f(z) and transcendental entire function g(z) in open plane have at least a Julia s direction .
证明了开平面上有限正级超越亚纯函数f(z)与超越整函数g(z)的复合函数φ(z)=f{g(z)},至少存在一条Julia方向。
3) integral transcendental function


整超越函数
4) transcendental semigroup


超越整函数半群
1.
We also obtain that for a finitely generated transcendental semigroup,there is a best generating set.
此外,超越整函数半群有着唯一的最小生成元集。
5) transcendental function


超越函数
1.
Design and implementation of floating-point operation unit with transcendental function;


支持超越函数的浮点运算单元的设计与实现
2.
The implementation of transcendental function in LSC87 coprocessor;


LSC87嵌入式协处理器中超越函数的实现方法
3.
Improved Genetic-annealing Algorithm's application in solving the nonlinear equations which Contains transcendental function
改进的遗传退火算法在针对含有超越函数的非线性方程组中求解的应用
6) permutable transcendental entire function


可交换的超越整函数
1.
Let f and g be two permutable transcendental entire functions.


令f和g是两个可交换的超越整函数 ,本文中我们首先证明对任正整数n和m ,J(f g)=J(fn gm) ,然后证明函数h(p(z) ) +az∈/B ,其中h(z)是任超越整函数 ,且h′(z) =0有无穷多个解 ,p(z)是一个多项式 ,且degp≥ 2 ,a(≠ 0 )∈C 。
补充资料:整函数
| 整函数 integral function 在整个复平面上处处解析的函数。整函数总可以在原点 展开成泰勒级数:  ,它在全平面收敛,整函数以∞点为唯一的孤立奇点,它在∞点的罗朗展式与它在原点的泰勒展式有一样的形式。当∞点是整函数的可去奇点时,这个整函数只能是常数,这就是著名的刘维尔定理,通常表述为“有界整函数必为常数”。利用这一定理可以得到代数基本定理的简单证明。当∞点是整函数的n阶极点时,这个整函数是一个n次多项式 ,也就是它的泰勒展式(或罗朗展式)只有有限多项。当∞点是整函数的本性奇点时,这个整函数的泰勒展式一定有无限多项,这类整函数称为超越整函数。由代数基本定理知道n次多项式一定有n个零点(也就是根),它总可以分解为n个一次因式的积,对于超越整函数,它可能有无限多个零点 ,比如sinπz就以全体整数为其零点集,也有的超越整函数没有零点,如ez就处处不为零,一般来说,没有零点的超越整函数总可以表成eg(z)的形式,此处g(z)也是一个整函数,而有无限多个零点的超越整函数f(z)也有一个因子分解式 ;形如 ,它在全平面收敛,整函数以∞点为唯一的孤立奇点,它在∞点的罗朗展式与它在原点的泰勒展式有一样的形式。当∞点是整函数的可去奇点时,这个整函数只能是常数,这就是著名的刘维尔定理,通常表述为“有界整函数必为常数”。利用这一定理可以得到代数基本定理的简单证明。当∞点是整函数的n阶极点时,这个整函数是一个n次多项式 ,也就是它的泰勒展式(或罗朗展式)只有有限多项。当∞点是整函数的本性奇点时,这个整函数的泰勒展式一定有无限多项,这类整函数称为超越整函数。由代数基本定理知道n次多项式一定有n个零点(也就是根),它总可以分解为n个一次因式的积,对于超越整函数,它可能有无限多个零点 ,比如sinπz就以全体整数为其零点集,也有的超越整函数没有零点,如ez就处处不为零,一般来说,没有零点的超越整函数总可以表成eg(z)的形式,此处g(z)也是一个整函数,而有无限多个零点的超越整函数f(z)也有一个因子分解式 ;形如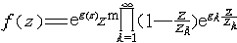 ,其中g(z)是整函数,0是m阶零点,zk是非零零点集,gk( ,其中g(z)是整函数,0是m阶零点,zk是非零零点集,gk( )是 )是 的多项式,这是魏尔斯托拉斯因子分解定理。超越整函数还有一个重要性质:若f(z)是超越整函数,则对任意复数A(包括A=∞),存在点列{zk },使zk 的多项式,这是魏尔斯托拉斯因子分解定理。超越整函数还有一个重要性质:若f(z)是超越整函数,则对任意复数A(包括A=∞),存在点列{zk },使zk  ∞(k ∞(k ∞)而有f(zk) ∞)而有f(zk) A。这一结果有一个更精确的发展:对超越整函数f(z),最多除去一个值(称为例外值)外,对所有其他的复数v值(v≠∞),f(z)-v都有无穷多个零点(毕卡定理)。 A。这一结果有一个更精确的发展:对超越整函数f(z),最多除去一个值(称为例外值)外,对所有其他的复数v值(v≠∞),f(z)-v都有无穷多个零点(毕卡定理)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条