1) Fermi-density-distribution with two parameters


双参数的费米密度分布
2) Fermi density distribution with two parameters


双参数费米密度分布函数
3) Fermi density distribution function with two parameters


双参数密度分布函数
4) Fermi distribution function


费米分布函数
5) Fermi distribution function


费密分布函数
6) two-parameter exponential distribution


双参数指数分布
1.
Fiducial interval estimation of two-parameter exponential distribution;


双参数指数分布的信仰区间估计
2.
Testing of a change-point in scale on two-parameter exponential distribution;


双参数指数分布尺度参数只有一个变点的检验
3.
In this paper,we used the concepts of the maximum likehood estimate and the direction maximum likehood estimate to give two kinds of estimates for two-parameter exponential distribution.
利用极大似然估计以及方向极大似然估计的概念,分别得到了双参数指数分布的参数的估计量,并证明了双参数指数分布中的两个参数满足双曲线型关
补充资料:费米-狄拉克分布
| 费米-狄拉克分布 Fermi-Dirac distribution 全同和独立的费米子系统中粒子的最概然分布。简称费米分布,量子统计中费米子所遵循的统计规律。由E.费米和P.A.M.狄拉克在1926年先后提出,故名。 费米子是 自旋为半整数( 即自旋为 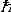 /2, /2,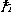 =h/2π,h是普朗克常量)的粒子,如轻子和重子,全同费米子系统中粒子不可分辨,费米子遵从泡利不相容原理,每一量子态容纳的粒子数不能超过一个。对于粒子数、体积和总能量确定的费米子系统,当温度为T时 ,处在能量为 =h/2π,h是普朗克常量)的粒子,如轻子和重子,全同费米子系统中粒子不可分辨,费米子遵从泡利不相容原理,每一量子态容纳的粒子数不能超过一个。对于粒子数、体积和总能量确定的费米子系统,当温度为T时 ,处在能量为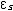 的量子态上的平均粒子数为 的量子态上的平均粒子数为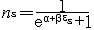
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |