1) metric space of fuzzy set
模糊集度量空间
1.
Specifically, existence, uniqueness and continuous dependence of fuzzy solutions for the fuzzy retarded integro-differential equation u·(t)=∫~t_0g(t,s,u(s))ds+f(t,x_t), where E~n is the set of all upper semi-continuous convex normal fuzzy numbers with bounded α-level set, f,g is continuous functions, are establish via Banach fixed-point theorem and the property of metric space of fuzzy set.
利用Banach不动点定理和模糊集度量空间的性质证明了这类方程解的存在性、惟一性和连续依赖性。
2) fuzzy valued metric space
模糊值度量空间
1.
Based on metrics d_i defined on reference [1] we consider the topological properies of fuzzy valued metric spaces(M[0,1],d i)(i=2,3),obtain the following conclusion:(M[0,1],d i)(i=2,3) are complete,connected,compact and separable metric spaces.
基于定义的度量 di ,研究模糊值度量空间 (M[0 ,1 ] ,di ) (i =2 ,3 )的拓扑性质 ,得到它们都是完备、连通、列紧和可分的度量空间的结论 。
2.
We introduce three kinds of metrics d i(i=1, 2, 3) in Fuzzy valued space M[0, 1], and consider the topological properties of fuzzy valued metric spaces( M [0, 1], d i)(i=1, 2, 3) .
在模糊值空间 M[0 ,1 ]上定义 3种度量 di(i=1 ,2 ,3) ,并讨论模糊值度量空间 (M[0 ,1 ] ,di) (i=1 ,2 ,3)的拓扑性
3) Fuzzy Metric Spaces
模糊度量空间
1.
Some properties on WF-fuzzy metric spaces(Ⅱ);
WF-模糊度量空间的若干性质(Ⅱ)
2.
Thus, the fixed point theorems for mappings of contractive type and locally contractive type on WF fuzzy metric spaces are established.
在 WF模糊度量空间中引入 Tρ 完备与 Tρ 完备等概念 ,证明了 Tρ 完备的 WF模糊度量空间上的 ( ψ)压缩映射与 ( ψ* )压缩映射存在惟一的不动点 ,两种局部压缩映射也存在不动点 。
4) fuzzy metric space
模糊度量空间
1.
n-dimensional Fuzzy Metric Space and Its Completeness;
n维模糊度量空间及其完备性
2.
In this paper, we obtain some common fixed point theorems under the condition of R-weakly commuting in fuzzy metric spaces and then extend these results to fuzzy 2 and 3-metric spaces.
讨论了模糊度量空间中在R-弱可换条件下的公共不动点存在性问题,并将此结果推广到模糊2-度量空间及模糊3-度量空间。
3.
This paper discusses some related concepts in fuzzy metric spaces, gives several important fixed point theorems of φcontrictive mappings with C property and non-expansive mappings in complete fuzzy metric spaces.
讨论了模糊度量空间中的相关概念 ,并给出了完备模糊度量空间中具有性质C的 φ压缩映象 ,以及一定条件下非扩张映象的不动点的存在性及唯一性的几个重要结果 ,这些结论是相关结论的推广 ,最后讨论了一个应用实
5) L-fuzzy metric space
L-模糊度量空间
6) Spatial Fuzzy Set
空间模糊集
补充资料：度量空间
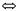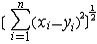| 度量空间 metric space 具有度量的抽象空间，设X是一个集合，若有定义在X×X上的非负实值函数d，满足①d（x，y）≥0，d（x，y）＝0  x＝y； ②d（x，y）＝d（y，x）；③d（x，z）≤d（x，y）＋d（y，z），则称（X，d）是度量空间，d称为距离或度量。这是最接近于欧几里得空间的抽象空间。利用度量可很自然地将欧几里得空间上点的邻域、开集、闭集，收敛序列以及连续映射等概念推广到一般度量空间，也能将一致连续的概念推广到度量空间。由于19世纪末集合论产生后，实变函数及泛函分析的发展，需要规定函数间的距离，因而抽象出度量、度量空间的概念，其创始人是M.R.弗雷歇。常见的度量空间有：n维欧几里得空间（Rn,d）：Rn＝｛（x1，…，xn）｜xi∈R，i＝1，2，…，n ｝，d（x，y）＝  ，其中x＝（x1，x2，…， xn），y＝（y1，y2，…，yn）。希尔 伯特空 间（l2；d）：l2＝｛（x1，x2，…，xn…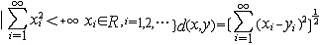）  ， 其中x ＝( x1，x2 ，…），y＝（y1，y2，…）∈l2。函数空间(ρ[0，1］，d)：C[0，1］＝｛f：f为[0，1］上的实值连续函数｝，对任意f，g∈C[0，1］，d(f，g)＝max｛｜f（x）－g（x）｜｝。 x∈[0，1］ 对度量空间（X，d）可引进拓扑结构，即以包含开球B（x，r）＝｛y∈X｜d（ x，y）＜r ｝的集为邻域定义拓扑，称为d所诱导的拓扑。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条