1) semantics of paradox


悖论语义
2) semantic paradox


语义悖论
1.
Research of semantic paradox through cyclical vibration function;


解决语义悖论的振荡周期函数模型——一种对语义悖论的可能解释
2.
The sentences that bring typical semantic paradoxes are all ambiguous.


本文由悖论非存在定理之引理推得一个重要推论———所谓“悖论”既有可能是非真非假的单义句也有可能是多义句 ,并进而论证了所有典型“语义悖论”均属后一种情况 ,根本就不是什么真正意义上的悖论 ,从而彻底修正了克里普克的有关理论。
3.
Every sentence causing a typical semantic paradox has the same meanings with it s negation and is also ambiguous.
导致典型语义悖论的语句同义于其否定,并且具有多种含义。
3) inconsistent with meaning


悖语义
4) distinction of semantic meaning


语义相悖
5) deontic paradox


道义悖论
1.
Based on a contrast between deontic paradox and moral paradox,argue that moral paradox is not a strictly logical paradox,but a moral quasi-paradox dilemma.
基于道义悖论与"道德悖论"的比较分析,论证后者不能归于严格的逻辑悖论,而应视作一种"类悖论道德困境";结合逻辑悖论社会文化功能的探讨,指明开展类悖论道德困境研究的重要价值。
2.
Deontic logic is a new realm of logic,deontic paradox is a new problem of deontic logic.


道义逻辑是逻辑学发展的新分支,道义悖论也因此成为一个全新的研究领域。
6) partial definition


悖论狭义
补充资料:悖论
| 悖论 paradox 自相矛盾的说法。即如果承认这个说法正确,就能推出这个说法不正确,反之,如果承认这个说法不正确,却又能推出这个说法正确。1900年前后在集合论中出现了一些悖论,例如罗素悖论和康托尔悖论。 ①罗素悖论。把所有满足条件x不属于x的集合x组成一个集合A,即 A是一切不属于自身的集合所组成的集合, A={x|x 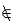 x}。在初期的集合论中,这样定义一个集合是允许的,既然承认A是一个集合,那么它是否满足A x}。在初期的集合论中,这样定义一个集合是允许的,既然承认A是一个集合,那么它是否满足A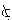 A?假定A A?假定A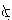 A,那么A属于所定义的集合,即A∈A,矛盾;假定A∈A,于是A不属于这样定义的集合,即A A,那么A属于所定义的集合,即A∈A,矛盾;假定A∈A,于是A不属于这样定义的集合,即A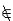 A,也自相矛盾。 A,也自相矛盾。②康托尔悖论。设V 是由一切集合所组成的集合。考虑集合V的基数 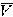 ,康托尔证明,V的幂集P(V)的基数 ,康托尔证明,V的幂集P(V)的基数 (V)大于 (V)大于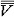 ;但根据V的定义,任何集合都是V的子集,因而不存在其基数大于 ;但根据V的定义,任何集合都是V的子集,因而不存在其基数大于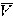 的集合,自相矛盾。 的集合,自相矛盾。这些悖论在当时震动了数学界。产生悖论的原因是那时的集合论本身还不够严格。为了避免悖论,数学家们重新研究集合的概念,进行严格整理,于是产生了多种集合论公理系统。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条