1) O(n)symmetricalfield φ~4 field model


O(n)对称φ4场论模型
2) O(N) symmetry


O(N)对称性
3) O(N) model


O(N)模型
1.
The infra-red renormalization properties of the O(N) model is studied to two loops.


利用一个与质量有关的重正化方案,研究了O(N)模型破缺相的红外重正化群性质。
4) φ4-theory


φ4理论
1.
It is suggested that the φ4-theory c.


提出φ4理论可以成为研究库仑系统问题的新方法。
5) asymmetrical typhoon model


非对称台风风场模型
6) symmetric models


对称模型
1.
The symmetric models for new linear equivalent form of C~2R;


C~2R新线性等价形式的对称模型
补充资料:场论
| 场论 fields,theory of 用向量分析研究数学、物理中有关问题的理论。在空间或空间的一部分Ω上分布着某种物理量,就构成一个场。例如物体的密度场、温度场;空间的引力场、流体的速度场等。尽管每种场都有各自的特性,但是在数量关系上各种场都有一定的数学形式,例如温度场是数量场,地球表面的地形可用“海拔”来刻画,这也是数量场,而引力场、速度场是向量场。 设W ?Â3,称函数 u:  为分布在Ω上的一个数量场,而称映射F: 为分布在Ω上的一个数量场,而称映射F: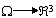 为分布在Ω上的一个向量场。在直角坐标系下,数量场可表为u(P)=u(x,y,z),其中(x,y,z)为P点的坐标,向量场可表为F(P)={F1,F2,F3},其中F1=F1(x,y,z),F2=F2(x,y,z),F3=F3(x,y,z),分别表示向量F(P)在X轴、Y轴和Z轴上的投影,引入坐标系是为了便于运算和进行数学处理,而场本身的性质与坐标系的选取无关。梯度、旋度、散度是场论中的三个基本量。 为分布在Ω上的一个向量场。在直角坐标系下,数量场可表为u(P)=u(x,y,z),其中(x,y,z)为P点的坐标,向量场可表为F(P)={F1,F2,F3},其中F1=F1(x,y,z),F2=F2(x,y,z),F3=F3(x,y,z),分别表示向量F(P)在X轴、Y轴和Z轴上的投影,引入坐标系是为了便于运算和进行数学处理,而场本身的性质与坐标系的选取无关。梯度、旋度、散度是场论中的三个基本量。设在W?Â3上分布着一个数量场u,且对每一P(x,y,z)∈Ω,有连续偏导数 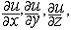 则称向量 则称向量 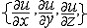 = =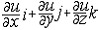 为数量场u在P点的梯度,记作gradu (P)。因此,数量场的梯度是一个向量场,梯度的方向是函数u(P)在P点变化率 最快(或最大)的方向。 为数量场u在P点的梯度,记作gradu (P)。因此,数量场的梯度是一个向量场,梯度的方向是函数u(P)在P点变化率 最快(或最大)的方向。设F=F(P)为向量场,在直角坐标系下,有F(P)={F1(x,y,z),F2(x,y,z),F3(x,y,z)}且 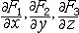 存在、连续,则称函数divF(P)= 存在、连续,则称函数divF(P)=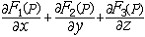 为F 的散度。因此,向量场的散度是一个数量场。假设F(P)是一个流体速度场,则当divF(P)>0时,表示 P 为流出的源,其值表示源的强度,当divF(P)<0时,表示P为吸收的洞,其值表示洞的强度,若divF(P)t=0,则P点既不是源,也不是洞,若在场内取一区域M,其边界 ¶M 为光滑曲面,¶M上任一点的外法线单位向量记为n ,则多元微积分中的高斯公式可表为 为F 的散度。因此,向量场的散度是一个数量场。假设F(P)是一个流体速度场,则当divF(P)>0时,表示 P 为流出的源,其值表示源的强度,当divF(P)<0时,表示P为吸收的洞,其值表示洞的强度,若divF(P)t=0,则P点既不是源,也不是洞,若在场内取一区域M,其边界 ¶M 为光滑曲面,¶M上任一点的外法线单位向量记为n ,则多元微积分中的高斯公式可表为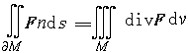
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |