1) q-Bose gas


q-玻色气体
1.
Basing on the Thomas-Fermi approximation or local density approximation(LDA) and the principle of the constancy of chemical potential in equilibrium,we calculate thermodynamic quantities of q-Bose gas,which include the critical temperature of BEC,the ground fraction of BEC,the total energy and the special heat of BEC.
基于Thomas-Fermi半经曲近似即局域密度近似和平衡态化学势为常数原理,计算了相对论q-玻色气体的热力学量,得到了玻色爱因斯坦凝聚的判据以及热容量跃变的判据,这不同于以往文献的理论结果。
2) Bose gas


玻色气体
1.
Thermodynamic properties of a weakly interacting Bose gas in a weak magnetic field;


弱磁场中弱相互作用玻色气体的热力学性质
2.
The influence of weak interaction on thermodynamic properties and the stability of imperfect Bose gas;
相互作用对玻色气体热力学性质及稳定性的影响
3.
Vortex solution of weak interacting Bose gases;


弱相互作用玻色气体的涡旋解
3) q-Boson


q-玻色子
4) Bose-condensed gas


玻色凝聚气体
1.
Relationship of the Gaussian width of Bose-condensed gas and the intensity of ID-optical lattices potential;
一维光晶格中玻色凝聚气体高斯宽度与光晶格势强度的关系
2.
Interference of Bose-condensed gas in a 1D optical lattice;


一维光晶格中玻色凝聚气体的干涉
3.
A solution to the ground and single vortex states of Bose-condensed gas in an axially symmetric harmonic trap;
轴对称谐振势阱中玻色凝聚气体基态和单涡旋态解
5) ideal Bose gas


理想玻色气体
1.
The general expressiones of energy and heat capacity of n-dimensional ideal Bose gas with differnet eneregy-momentum relations are obtained at temperature T>T C and T<T C .
给出了T>TC和T<TC情况下不同能谱的n维简并理想玻色气体的内能及热容量的普遍表达式,应用于三维极端相对论理想玻色气体时则在T=TC处热容量CV出现跃变,这与通常玻色气体的CV在TC处连续的结果不同。
6) generalized Bose gas


广义玻色气体
1.
By using the generalized Bose-Einstein distribution function,Bose-Einstein condensation of a generalized Bose gases trapped in a generic power-law potential in the two dimensional space is investigated.
应用广义玻色-爱因斯坦分布函数研究在幂函数外势中二维广义玻色气体的玻色-爱因斯坦凝聚(BEC),导出二维广义玻色气体的临界温度、基态粒子占据率和热容量等物理量的解析表达式,讨论了非广延参数q对玻色系统热统计性质的影响。
补充资料:玻色-爱因斯坦分布
| 玻色-爱因斯坦分布 Bose-Einstein distribution 全同和独立的玻色子系统中粒子的最概然分布。简称玻色分布,量子统计中玻色子所遵从的统计规律。玻色-爱因斯坦分布是S.N.玻色和A.爱因斯坦在1924年先后提出来的,故名。 玻色子是自旋为整数的粒子,如光子、a 粒子等,全同玻色子系统中粒子不可分辨,玻色子不遵从泡利不相容原理,每一量子态所能容纳的粒子数不受限制。对于粒子数、体积和总能量确定的玻色子系统,当温度为T时,处在能量为εs的量子态上的平均粒子数为 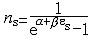
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |