1) Cocycle
[kə'saikl]


余循环
1.
Assuming that H is a Hopf algebra o ver a f ield k ,A a right H comodale algebra, σ ∈Hom k ( H ? 獺 , k )is an invertible right 2 cocycle of H ,we define a new multiplication in A and get a twisted alge bra A σ .
设H是域k上的Hopf代数,σ∈Homk(HH,k)是H的可逆的右2-余循环,A是k上的H-余模代数。
2) cocyclc comodulle


余循环余模
3) two-cocycle


2-余循环
4) strong cocycle


强余循环
1.
If H is a bialgebra over a field k,and σ∈(H×H) * is a strong cocycle,then we can prove the existence of a sub monoidal category μ (H,σ) in μ H ,and several equivalent conditions of μ (H,σ) =μ H .
σ∈ (H× H ) *是强余循环 ,本文证明在 m onoidal范畴μH中存在一个辫子 m onoidal子范畴μ( H ,σ) 。
5) reduancy cycle


余码循环
6) 1-cocycle


1-余循环
1.
Based on the different classification of 1-cocycle of the group algebra over dihedral group,the algebra relationship and the Hopf algebra structure of the Hopf Ore extension are provided under the condition of odd and even numbers.
利用二面体群群代数上的1-余循环的不同分类,明确给出了在奇数和偶数两种情形下,二面体群群代数的Hopf Ore扩张的代数关系及其Hopf代数结构。
补充资料:循环系统的进化鱼的循环系统
李瑞端绘
[图]
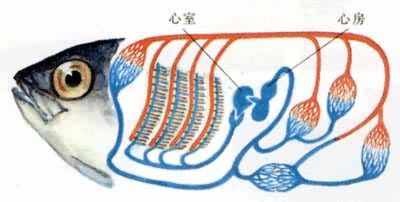
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条