2) nonlinear semi-Fredholm operator


非线性半Fredholm算子
3) linear operator semigroup


线性算子半群
1.
The observer design for linear neutral delay systems(NDSs)is investigated based on the spectral decom-position theory of linear operator semigroup.
针对线性中立型时滞系统,利用线性算子半群的谱分解理论进行观测器设计。
4) semi-nonlinear operator equation


半线性算子方程
1.
The existence of solution for semi-nonlinear operator equation is studied by using Initial Value Problem(IVP) method.
使用常微分方程初值问题(IVP)方法讨论了半线性算子方程Lu+N[u]=F(u)是否有解。
5) nonlinear Lipschitzian semigroup


非线性Lipschitz算子半群
6) C0 semigroups of bounded linear operators


有界线性算子C0半群
补充资料:线性算子
| 线性算子 linear operator 具有线性性质的一类映射。算子是函数概念的发展和拓广,设X,Y 为数域K上的线性空间,以D(T)Ì蘕为定义域,取值于Y 的映射统称为算子。进而,若D(T)为线性子集,算子T具有线性性质:"x ,y∈D(T),"a ,β∈K ,有T(ax+βy)=aT(x)+βT(y),则称T为线性算子。熟悉的积分算子Tf(x)= 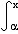 f(t)dt,"f∈C[a,b]={f:f为定义在[a,b]上的连续函数}是从C[a,b]到自身的线性算子,微分算子是 f(t)dt,"f∈C[a,b]={f:f为定义在[a,b]上的连续函数}是从C[a,b]到自身的线性算子,微分算子是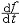 从 从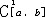 ={f:f为定义在[a,b]上具有一阶连续导数的连续函数}到C[a,b] 的线性算子。线性算子是线性泛函分析研究的基本对象之一,若X、Y为线性赋范空间,则可利用线性关系简化对连续性的讨论,此外,有限维空间上的线性算子必定连续,并且对线性算子来说,其连续性与有界性是等价的。 ={f:f为定义在[a,b]上具有一阶连续导数的连续函数}到C[a,b] 的线性算子。线性算子是线性泛函分析研究的基本对象之一,若X、Y为线性赋范空间,则可利用线性关系简化对连续性的讨论,此外,有限维空间上的线性算子必定连续,并且对线性算子来说,其连续性与有界性是等价的。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条