1) parabolic system


抛物系统
1.
The stability of a delayed stage-structured parabolic system with feedback controls;


一类具反馈控制和时滞阶段结构抛物系统的稳定性
2.
Behaviors of solutions to a parabolic system describing a cooperating model with nonlocal sources;
具有非局部源的互惠模型抛物系统解的性质
3.
Blowing up of nonnegative classical solution to a parabolic system;


一个抛物系统非负古典解的爆破
2) parabolic systems


抛物系统
1.
Identifications of parameters in parabolic systems;


抛物系统的参数识别问题(英文)
3) paraboloid system


抛物面系统
4) parabolic system


抛物型系统
1.
Global exponential stability for parabolic systemswith continuous distributed delays;


连续分布时滞抛物型系统的全局指数稳定性
5) periodic parabolic system


周期抛物系统
6) semilinear parabolic system


半线性抛物系统
1.
This work is concerned with the local null controllability for a coupled semilinear parabolic systems describing a kind of biological and chemical process.
讨论了一类具有生态学和化学背景的半线性抛物系统的局部零能控性,利用Carleman不等式和Kakutani不动点定理研究了线性化系统的零能控性和原系统的局部零能控性。
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 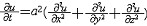 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式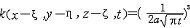 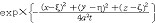 热传导方程初值问题的解可用基本解叠加而成,即 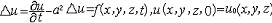 的解为 的解为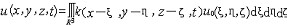 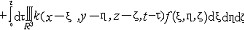 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 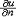 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条