1) z circular matrix


Z循环矩阵
1.
The general elements of inverse matrix of z circular matrix are extracted with the help of Vandermonde s matrix, then simplified by means of the summertric polynomial σ_1, σ_2…σ_n of the "n" radical roots of the equation, x~(?)-Z=0.
本文先利用范德蒙矩阵求得Z循环矩阵逆矩阵的一般元素,然后利用方程x~(?)-z=0的n个根的对称多项式σ_1、σ_2、…、σ_n予以简化。
2) Z-Circulant Matrix


Z-循环矩阵
3) Zcirculant lumped matrix


Z-循环分块矩阵
4) Z-Basic Circulant Matrix


Z-基本循环矩阵
5) symmetric Zcirculant lumped matrix


对称Z-循环分块矩阵
6) circulant matrices


循环矩阵
1.
Eigenvalues of a kind of circulant matrices and its application on subdivision;


一类循环矩阵的特征值及其在细分方法中的应用
2.
VLSI decoding design of low-density parity-check codes based on circulant matrices


基于循环矩阵的低密度校验码的VLSI译码设计
3.
Making use of some relations between discrete Fourier transformation and convolution, I give a sufficiency and necessary condition which estimates that a matrix is a circulant matrix, and give concretely an accounting formula of m-orders circulant matrices.
利用离散Fourier变换与卷积的关系,给出了判断一个矩阵为循环矩阵的充要条件,并具体给出了一种求循环矩阵的m次幂通项的计算公式。
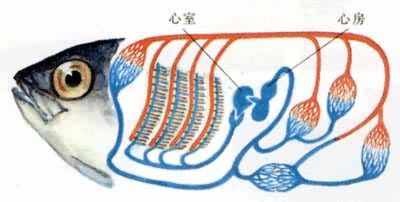
补充资料:循环系统的进化鱼的循环系统
李瑞端绘
[图]
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条