1) (m) power proportion


(m次)幂比例
3) m-orders


m次幂
1.
General Terms of m-orders Circulant Matrices;


循环矩阵的m次幂的通项
4) inverse power proportion


反幂比例
5) m-th power part


m次幂部分数列
1.
On the mean values of m-th power part and Smarandache ceil function;


关于m次幂部分数列与Smarandache ceil函数的均值
6) p~m power matrix


P~m次幂矩阵
补充资料:幂
| 幂 power 表示一个数自乘若干次的形式。ab称为a的b次幂。其中a称为这个幂的底数,b称为这个幂的指数。这里乘方的含义随着指数b所在范围不同而有不同的规定。① 当b是正整数n时,an称为正整数指数幂,表示n个a连乘的结果,即 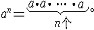 ②当b是负整数-n且a≠0时,a-n称为负整数指数幂,规定 ②当b是负整数-n且a≠0时,a-n称为负整数指数幂,规定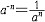 ,即 ,即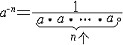 ③当b=0且 ③当b=0且 ≠0时, ≠0时, 0称为 0称为 的零次幂,规定 的零次幂,规定 0=1。④ 当b为正分数m/n(m,n都是正整数,且n>1)时,限定 0=1。④ 当b为正分数m/n(m,n都是正整数,且n>1)时,限定 ≥0,规定 ≥0,规定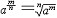 ,称为a的正分数指数幂 。⑤当b是负分数-(m ,n为正整数,且n>1)时,限定 ,称为a的正分数指数幂 。⑤当b是负分数-(m ,n为正整数,且n>1)时,限定 >0,规定 >0,规定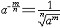 ,称为 ,称为 的负分数指数幂。⑥当b是无理数 的负分数指数幂。⑥当b是无理数 ,且 ,且 >0时,aa称为a的无理数指数幂,对正无理数 >0时,aa称为a的无理数指数幂,对正无理数 ,取有理数列{ ,取有理数列{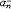 }和{ }和{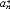 }, }, 和 和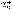 分别是 分别是 的精确到1/10n的不足近似值和过剩近似值 。有理数指数幂 的精确到1/10n的不足近似值和过剩近似值 。有理数指数幂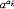 和 和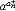 已经有了定义,于是规定 已经有了定义,于是规定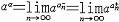 ,即aa用两个数列{ ,即aa用两个数列{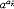 }和{ }和{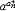 }的共同极限确定。对于负无理数- }的共同极限确定。对于负无理数- ,规定 ,规定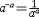 。 。这样,对幂指数由正整数到无理数各种情况,幂的概念都有了规定。从而,任意实数指数幂都有确切的含义。实数指数幂的运算法则有:①  a· a· β= β= a +β;②( a +β;②( a) β= a) β= aβ;③( aβ;③( b)a= b)a= aba。式中 aba。式中 >0,b>0; >0,b>0; ,β为任意实数,这与正整数指数幂的运算法则相同。 ,β为任意实数,这与正整数指数幂的运算法则相同。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条