1) 2-D wavelet transform
2-D小波变换
2) NO·_2
NO·2
3) "2+2"
“2+2”
1.
Analysis of the Current Situation of "2+2" Training Way and Research on Managing Model;
军校“2+2”组训方式现状分析及其管理教育模式研究
4) "2×2×2"
“2×2×2”
5) 2+2+2
“2+2+2”
1.
An important background of our present banking reform is that we are undergoing banking market entry, which has the characteristics of "2+2+2".
当前我国银行业改革的一个重要背景,就是面临具有“2+2+2”特点的市场进入。
6) 22-out-of-2
2乘2取2
参考词条
2-范数‖‖_2
“2+2”模式
Pb~(2+)、Cd~(2+)
Mg~(2+)/Ca~(2+)
HCl+2、HBr+2
K_(2、2、r)
[2+2+2]环三聚
[2+2+2]环加成
Cu~(2+)、Pb~(2+)、Cd~(2+)
(2+2+2)环加成
Ag~(2+)
Mn~(2+)
UO_2~(2+)
Zn~(2+)
Cd~(2+)
Ni~(2+)
溃疡愈合质量
恩琴
补充资料:波
波
wave
某一物理量的扰动或振动在空间逐点传递时形成的运动。不同形式的波虽然在产生机制、传播方式和与物质的相互作用等方面存在很大差别,但在传播时却表现出多方面的共性,可用相同的数学方法描述和处理。
波的产生及其类别 波动是物质运动的重要形式,广泛存在于自然界。被传递的物理量扰动或振动有多种形式,机械振动的传递构成机械波 ,电磁场振动的传递构成电磁波(包括光波),温度变化的传递构成温度波(见液态氦),晶体点阵振动的传递构成点阵波(见点阵动力学),自旋磁矩的扰动在铁磁体内传播时形成自旋波(见固体物理学),实际上任何一个宏观的或微观的物理量所受扰动在空间传递时都可形成波。最常见的机械波是构成介质的质点的机械运动(引起位移、密度、压强等物理量的变化)在空间的传播过程,例如弦线中的波、水面波、空气或固体中的声波等。产生这些波的前提是介质的相邻质点间存在弹性力或准弹性力的相互作用,正是借助于这种相互作用力才使某一点的振动传递给邻近质点,故这些波亦称弹性波。电磁场的振动在空间传递时依靠的是电磁场本身的规律,毋需任何介质的存在,故电磁波(包括光波)可在真空中传播。振动物理量可以是标量,相应的波称为标量波(如空气中的声波),也可以是矢量,相应的波称为矢量波(如电磁波)。振动方向与波的传播方向一致的称纵波,相垂直的称横波。
波的共同特性 各种形式的波的共同特征是具有周期性。受扰动物理量变化时具有时间周期性,即同一点的物理量在经过一个周期后完全恢复为原来的值;在空间传递时又具有空间周期性,即沿波的传播方向经过某一空间距离后会出现同一振动状态(例如质点的位移和速度)。因此,受扰动物理量u既是时间t,又是空间位置r的周期函数,函数u(t,r)称为波函数或波动表示式,是定量描述波动过程的数学表达式。广义地说,凡是描述运动状态的函数具有时间周期性和空间周期性特征的都可称为波,如引力波,微观粒子的概率波(见波粒二象性)等。
各种波的共同特性还有:①在不同介质的界面上能产生反射和折射,对各向同性介质的界面,遵守反射定律和折射定律(见反射定律、折射定律);②通常的线性波叠加时遵守波的叠加原理(见光的独立传播原理);③两束或两束以上的波在一定条件下叠加时能产生干涉现象(见光的干涉);④波在传播路径上遇到障碍物时能产生衍射现象(见光的衍射);⑤横波能产生偏振现象(见光的偏振)。
简谐波 简谐振动在空间传递时形成的波动称为简谐波,其波函数为正弦或余弦函数形式。各点的振动具有相同的频率v,称为波的频率,频率的倒数为周期,即T=1/v。在波的传播方向上振动状态完全相同的相邻两个点间的距离称为波长,用λ表示,波长的倒数称波数。单位时间内扰动所传播的距离u称为波速 。波速、频率和波长三者间的关系为u=vλ。波速与波的种类和传播介质的性质有关。例如空气中的声波波速为
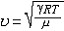 r为绝热指数(见绝热过程),R为气体常数,μ为摩尔质量,T为热力学温度;细杆中纵波波速为
r为绝热指数(见绝热过程),R为气体常数,μ为摩尔质量,T为热力学温度;细杆中纵波波速为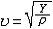 ρ为质量密度 ,Y为杆的弹性模量;杆中的横波波速为
ρ为质量密度 ,Y为杆的弹性模量;杆中的横波波速为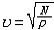 Ν为杆的切变模量。电磁波的波速为
Ν为杆的切变模量。电磁波的波速为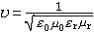 ,ε0和μ0为真空的电容率和磁导率,εr和μr为介质的相对电容率和相对磁导率。在同一介质中,不同频率的波有不同的波速,此称为频散,在光学中叫色散(见光的色散)。为写出简谐波的波函数,设坐标原点的振动表示式为u(t)=Acosωt,A为原点的振幅,ω为圆频率,它与频率的关系为ω=2πv ,则空间任一点的振动可表示为
,ε0和μ0为真空的电容率和磁导率,εr和μr为介质的相对电容率和相对磁导率。在同一介质中,不同频率的波有不同的波速,此称为频散,在光学中叫色散(见光的色散)。为写出简谐波的波函数,设坐标原点的振动表示式为u(t)=Acosωt,A为原点的振幅,ω为圆频率,它与频率的关系为ω=2πv ,则空间任一点的振动可表示为
u(t,r)=A(r)cos[ωt-j(r)]
wave
某一物理量的扰动或振动在空间逐点传递时形成的运动。不同形式的波虽然在产生机制、传播方式和与物质的相互作用等方面存在很大差别,但在传播时却表现出多方面的共性,可用相同的数学方法描述和处理。
波的产生及其类别 波动是物质运动的重要形式,广泛存在于自然界。被传递的物理量扰动或振动有多种形式,机械振动的传递构成机械波 ,电磁场振动的传递构成电磁波(包括光波),温度变化的传递构成温度波(见液态氦),晶体点阵振动的传递构成点阵波(见点阵动力学),自旋磁矩的扰动在铁磁体内传播时形成自旋波(见固体物理学),实际上任何一个宏观的或微观的物理量所受扰动在空间传递时都可形成波。最常见的机械波是构成介质的质点的机械运动(引起位移、密度、压强等物理量的变化)在空间的传播过程,例如弦线中的波、水面波、空气或固体中的声波等。产生这些波的前提是介质的相邻质点间存在弹性力或准弹性力的相互作用,正是借助于这种相互作用力才使某一点的振动传递给邻近质点,故这些波亦称弹性波。电磁场的振动在空间传递时依靠的是电磁场本身的规律,毋需任何介质的存在,故电磁波(包括光波)可在真空中传播。振动物理量可以是标量,相应的波称为标量波(如空气中的声波),也可以是矢量,相应的波称为矢量波(如电磁波)。振动方向与波的传播方向一致的称纵波,相垂直的称横波。
波的共同特性 各种形式的波的共同特征是具有周期性。受扰动物理量变化时具有时间周期性,即同一点的物理量在经过一个周期后完全恢复为原来的值;在空间传递时又具有空间周期性,即沿波的传播方向经过某一空间距离后会出现同一振动状态(例如质点的位移和速度)。因此,受扰动物理量u既是时间t,又是空间位置r的周期函数,函数u(t,r)称为波函数或波动表示式,是定量描述波动过程的数学表达式。广义地说,凡是描述运动状态的函数具有时间周期性和空间周期性特征的都可称为波,如引力波,微观粒子的概率波(见波粒二象性)等。
各种波的共同特性还有:①在不同介质的界面上能产生反射和折射,对各向同性介质的界面,遵守反射定律和折射定律(见反射定律、折射定律);②通常的线性波叠加时遵守波的叠加原理(见光的独立传播原理);③两束或两束以上的波在一定条件下叠加时能产生干涉现象(见光的干涉);④波在传播路径上遇到障碍物时能产生衍射现象(见光的衍射);⑤横波能产生偏振现象(见光的偏振)。
简谐波 简谐振动在空间传递时形成的波动称为简谐波,其波函数为正弦或余弦函数形式。各点的振动具有相同的频率v,称为波的频率,频率的倒数为周期,即T=1/v。在波的传播方向上振动状态完全相同的相邻两个点间的距离称为波长,用λ表示,波长的倒数称波数。单位时间内扰动所传播的距离u称为波速 。波速、频率和波长三者间的关系为u=vλ。波速与波的种类和传播介质的性质有关。例如空气中的声波波速为
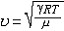 r为绝热指数(见绝热过程),R为气体常数,μ为摩尔质量,T为热力学温度;细杆中纵波波速为
r为绝热指数(见绝热过程),R为气体常数,μ为摩尔质量,T为热力学温度;细杆中纵波波速为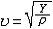 ρ为质量密度 ,Y为杆的弹性模量;杆中的横波波速为
ρ为质量密度 ,Y为杆的弹性模量;杆中的横波波速为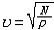 Ν为杆的切变模量。电磁波的波速为
Ν为杆的切变模量。电磁波的波速为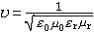 ,ε0和μ0为真空的电容率和磁导率,εr和μr为介质的相对电容率和相对磁导率。在同一介质中,不同频率的波有不同的波速,此称为频散,在光学中叫色散(见光的色散)。为写出简谐波的波函数,设坐标原点的振动表示式为u(t)=Acosωt,A为原点的振幅,ω为圆频率,它与频率的关系为ω=2πv ,则空间任一点的振动可表示为
,ε0和μ0为真空的电容率和磁导率,εr和μr为介质的相对电容率和相对磁导率。在同一介质中,不同频率的波有不同的波速,此称为频散,在光学中叫色散(见光的色散)。为写出简谐波的波函数,设坐标原点的振动表示式为u(t)=Acosωt,A为原点的振幅,ω为圆频率,它与频率的关系为ω=2πv ,则空间任一点的振动可表示为u(t,r)=A(r)cos[ωt-j(r)]
说明:补充资料仅用于学习参考,请勿用于其它任何用途。