1) 1-D bandlimited Weierstrass fractal rough surface
一维带限Weierstrass分形粗糙面
2) 2-D fractal rough surface
二维分形粗糙面
1.
Fast computation of electromagnetic scattering characteristics for 2-D fractal rough surface by SMFSIA/CAG
SMFSIA/CAG快速计算二维分形粗糙面的电磁散射特性
3) Fractal rough surface
分形粗糙面
1.
The convergence for this method is proved and applied to solve inverse problem of fractal rough surface.
最后将这一算法运用于分形粗糙面的反演问题中,得到了很好的反演效果。
2.
To effectively numerically simulate bistatic scattering from a penetrable permittivity dielectric (as high as (25+i1 0) ε 0) fractal rough surface at low grazing angle, a dense grid is required for accuracy; but a dense grid requires a large central processing unit (CPU) and memory.
对于高介电常量分形粗糙面的双站散射与透射的数值计算 ,须用密网格来剖分粗糙面 ,这样就产生了计算内存大和计算时间长的问题 。
3.
In order to numerically simulate bistatic scattering from fractal rough surface at low grazing angle incidence, a hybrid approach of the forward-backward method (FBM) with spectral\|accelerated algorithm (SAA) is developed to solve the magnetic field integral equation.
为模拟复杂分形表面特别是在低掠角入射条件下的双站散射 ,发展了一种结合前后向迭代方法 (FBM)与谱加速算法 (SAA)快速求解散射场的MonteCarlo数值方法 ,计算了在TE ,TM锥形波入射在一维分形导体粗糙面的双站散射以及有规则异物存在时的双站散射 ,讨论了分形粗糙面双站散射的角度性分布与其分数维的关系 。
4) 2-D fBm fractal rough surface
二维fBm分形粗糙面
1.
A 2-D fBm fractal rough surface is used to simulate the natural rough surface of layered medium,and the formulae of the scattering coefficient of the 2-D fBm fractal dielectric rough surface of layered medium with the plane wave incidence is derived by using the small perturbation method in association with the power spectrum density of 2-D fBm fractal rough surface.
采用二维fBm分形粗糙面来模拟实际的分层介质粗糙面,结合二维fBm分形粗糙面的功率谱导出了平面波入射二维fBm分形分层介质粗糙面的散射系数计算公式。
5) One-dimensional Random Rough Surface
一维随机粗糙面
1.
One-dimensional Random Rough Surface Scattering of Electromagnetic
一维随机粗糙面的电磁散射研究
6) fractal rough surface
分形粗糙表面
1.
To investigate the backscattering enhancement effect of fractal rough surface,the method of moment associated with the tapering incident wave is adopted.
针对粗糙表面散射实验中的后向散射增强现象,采用锥形波束入射的矩量法定量计算了分形粗糙表面的后向散射增强效应,研究了波形参数和表面尺寸的匹配问题,分析了不同入射角下散射增强的角宽度,比较了不同分维数和表面模型下散射增强的幅值。
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 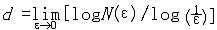 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条