1) General continuum hypothesis(GCH)


广义连续统假设(GCH)
2) general continuum hypothesis


广义连续统假设
3) continuum hypothesis


连续统假设
1.
The structural stabilitycorresponds to computability; the continuum hypothesis connotes the structural stability; and the formalthought structurally stable.
连续统假设是对结构稳定性的承诺。
2.
Especially from the F cardinality, some new ideas on the continuum hypothesis are shown.


以模糊映射为基础给出了模糊集基数的定义,不但得到了有关基数的大部分结论,而且有其自身的特有性质;特别对于连续统假设这一世界难题可能有新的启示。
4) Continuum hypothesis(CH)


连续统假设(CH)
5) continuous singular system


连续广义系统
1.
Non-fragile H_∞ control for continuous singular systems with state delay and uncertainties;
带有状态滞后和不确定性的连续广义系统的非脆弱H_∞控制
补充资料:连续统假设
| 连续统假设 continuum hypothesis 数学上关于连续统势的假设。常记作CH。通常称实数集即直线上点的集合为连续统,而把连续统的势(大小)记作C。2000多年来,人们一直认为任意两个无穷集都一样大。直到1847年,G.康托尔证明:任何一个集合的幂集(即它的一切子集构成的集合)的势都大于这个集合的势,人们才认识到无穷集合也可以比较大小。自然数集是最小的无穷集合,自然数集的势记作 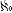 。康托尔证明连续统势等于自然数集的幂集的势。是否存在一个无穷集合,它的势比自然数集的势大,比连续统势小?这个问题被称为连续统问题。康托尔猜想这个问题的解答是否定的,即连续统势是比自然数集的势 。康托尔证明连续统势等于自然数集的幂集的势。是否存在一个无穷集合,它的势比自然数集的势大,比连续统势小?这个问题被称为连续统问题。康托尔猜想这个问题的解答是否定的,即连续统势是比自然数集的势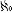 大的势中最小的一个无穷势,记作 大的势中最小的一个无穷势,记作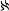 1。这个猜想就称为连续统假设。1938年,K.哥德尔证明了CH对ZF公理系统(见公理集合论)是协调的,1963年,P.J.科恩是不可能判定真假的。证明CH对ZF公理系统是独立的。这样,在ZF公理系统中,CH是不可能判定真假的。 1。这个猜想就称为连续统假设。1938年,K.哥德尔证明了CH对ZF公理系统(见公理集合论)是协调的,1963年,P.J.科恩是不可能判定真假的。证明CH对ZF公理系统是独立的。这样,在ZF公理系统中,CH是不可能判定真假的。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条