1) pseudoparabolic


拟抛物
1.
Global existence and asymptotic behavior for nonlinear pseudoparabolic equations;


拟抛物方程初边值问题的整体解与渐近性态
2) pseudo-parabolic


拟抛物
1.
With the continous semi-group method,we have proved in this paper that there isno regularization effect for the pseudo-parabolic equations.
运用连续半群方法说明了拟抛物方程不存在正则化效应,此结果揭示了拟抛物方程与抛物型方程的一个本质性差别。
3) parabola fitting


抛物线拟合
1.
A new sub-pixel algorithm based on the principle of the parabola fitting is proposed.


本文提出了一种新颖的基于抛物线拟合原理的亚像素求取算法。
2.
The sub-pixel edge point is then calculated by parabola fitting of the luminance of all pixel points near a pixel-level edge point in a certain range of horizontal or vertical direction.
在十字亮条有用区域内,首先利用局域亮度极大方法检测亮条像素级屋脊边缘点;然后提取像素级边缘点水平或垂直方向上一定范围内的像素点亮度进行抛物线拟合,计算亚像素边缘点坐标;最后利用最小二乘法拟合出两条直线,计算十字交点及横亮线倾角。
4) paraboloid fitting


抛物面拟合
5) parabola of fit


拟合抛物线
6) quasi_paraboloid


拟抛物面规则
1.
With the rules of quasi_paraboloid, the Gibbs energy of O ′-sialon was estimated.


采用拟抛物面规则预报了O′-sialon的标准生成Gibbs自由能。
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 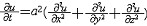 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式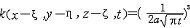 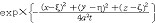 热传导方程初值问题的解可用基本解叠加而成,即 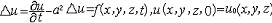 的解为 的解为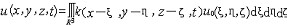 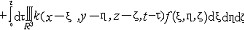 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 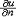 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条