1) quasi-parabolic Navier-Stokes equations


拟抛物N-S方程
2) 3D parabo-lized N-S equations


抛物化三维N-S方程
3) N's equations of numerical simulation


N-S方程模拟
4) quasi-linear parabolic equation


拟线性抛物方程
1.
Extinction of a quasi-linear parabolic equation is considered.


讨论了一类拟线性抛物方程柯西问题与初边值问题解的耗竭现象 ,给出了解在有限时刻出现耗竭的条件 ,并对耗竭时刻的上限进行了估计。
5) quasilinear parabolic equation


拟线性抛物方程
1.
The blow-up of the solution of the quasilinear parabolic equation;


一类拟线性抛物方程解的爆破
2.
The blow-up of solution for a class of quasilinear parabolic equation with source termand positive initial energy is studied by the well potential and the cocavity methods.
利用位势井方法和凸性方法得到了一类具源项和正初始能量的拟线性抛物方程解的不存在性,推广了已知结果。
6) Quasilinear Pseudo-Parabolic Equation


拟线性拟抛物方程
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 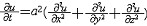 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式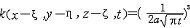 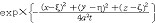 热传导方程初值问题的解可用基本解叠加而成,即 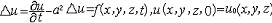 的解为 的解为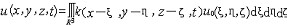 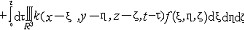 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 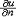 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条