1) parabolic source


抛物型声源
3) parabolic
[英][,pærə'bɔlik] [美][,pærə'bɑlɪk]


抛物型
1.
Necessary and sufficient condition for oscillations of nonlinear parabolic partial differential equations;
非线性抛物型时滞微分方程解振动的充要条件
2.
Oscillatory properties of solutions of certain delayed parabolic partial differential equations are investigated.
讨论了一类多滞量延迟时滞抛物型偏微分方程解的振动性质 ,利用平均值方法将所讨论的偏微分方程转化为时滞微分方程的问题 ,获得了其一切解振动的充要条件 ;所得的条件将时滞偏微分方程解的振动判别问题转化为时滞微分方程解的振动判别问题 ;结果充分显示了解的振动是由时滞量引起的 ,指出了其与普通抛物型偏微分方程解的质的差异 ;同时也指出了时滞在振动中的影响作用以及时滞偏微分方程解的振动性质在生物学、医学、工程学、化学、物理学等学科中的广泛应
3.
Using the methods of regularization and prior estimation, the author proves the existence of global solution of a nonlinear parabolic equation as long as the nonlinear function f(x,t,u, u ) satisfies the conditions of structure and smoothing and the initial value function is small.
在非线性函数f(x,t,u , u)同时含有未知函数u与它的梯度 u ,以及x ,t的某个已知函数 φ(x,t)的情形下 ,运用正则化和先验估计的方法得到结论 :只要函数f(x ,t,u , u)满足结构性条件和某些光滑性条件 ,初值函数u0 (x)适当小 ,非线性抛物型方程的初边值问题的整体解必定存在 ,且给出了解的衰减估计 。
4) parabola
[英][pə'ræbələ] [美][pə'ræbələ]


抛物线型
1.
By introducing the characteristic of new technologies about bubbling atomizing small oil gun, direct firing parabola burners of pulverized coal,large size duff store\|house, the author shows the application foreground and advantage of technique and economy about these new technology on old 125 MW,200 MW set in the new electrovalency policy.
通过介绍电厂锅炉的气泡雾化小油枪、抛物线型煤粉直接点火燃烧器、大容量煤粉仓蓄能等新技术的特点 ,说明在新电价政策下 ,一些 1 2 5MW、2 0 0MW老机组采用这些新技术的应用前景及技术经济优
5) parabolical wave


抛物型波
6) parabolic type


抛物型
1.
Through discussing the singular perturbed problem of parabolic type and first-order hyperbolic type in partial differential equations,this paper puts forward a boundary layer format without losing its characteristics.
通过对抛物型偏微分方程和一阶双曲型偏微分方程奇异摄动问题的讨论,提出了在使边界层的特性不至于丧失的前提下的边界层格式。
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 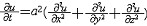 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式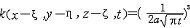 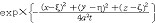 热传导方程初值问题的解可用基本解叠加而成,即 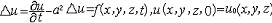 的解为 的解为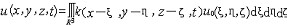 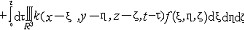 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 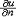 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条