1) claw free


无爪
1.
Two new sufficient conditions for hamiltonian claw free graphs are given.


给出了关于无爪Hamilton图的两个新的充分条件 ,其结果可推出一些已知的结果 ,在某种意义下 ,条件是最好可能的 。
2) claw-free graph


无爪图
1.
Hamiltonicity,neighborhood union and square graphs of claw-free graphs;


哈密尔顿性、邻域并和无爪图的平方图(英文)
2.
A note charaterization of the claw-free graphs;


关于无爪图特征的一个注记
3.
An implicit degree condition for Hamiltonian cycles in k-connected claw-free graphs;


k-连通无爪图中存在哈密尔顿圈的一个隐度条件
3) claw-free graphs


无爪图
1.
The edge-number of maximum spanning eulerian subgraphs of claw-free graphs;


无爪图的极大欧拉生成子图边数问题
2.
Circumference in three-connected claw-free graphs;


3-连通无爪图的最长圈
3.
Hamilton problem of 2-connected claw-free graphs;


2-连通无爪图的Hamilton性
4) claw free graph


无爪图
1.
In this paper, we will use the technique of the vertex insertion on l connected ( l=k or k+1,k≥2 ) claw free graphs to provide a unified proof for G to be hamiltonian or 1 hamiltonian, the sufficient conditions are expressed by the inequality concerning ∑ki=0N(Y i) and n(Y) for eac.
本文利用插点方法 ,给出了关于k或 (k + 1)连通 (k≥ 2 )无爪图G是哈密尔顿的或 1哈密尔顿的统一的证明 。
2.
It is supposed that P[u,v] is the longest path of a 2 connected claw free graph G,d P(x β,x α)=︱P[x β,x α]︱-1,(x β<x α),d * P(x α,x β)=︱P[x α,x β]︱-1(x α<x β ).
若P[u ,v]是 2连通无爪图G的最长路 ,设dp(xβ,xα) =︱P[xβ,xα]︱ -1 (xβ无爪图 ,且G的每个导出子图A ,A1都满足 φ(a1,a2 ) ,则G是Hamilton
3.
It was proved that if G is a 3 connected claw free graph on n vertices with the minimum degree δ =min{d( x )| x ∈ V(G )}and δ *=min{max(d( x ),d( y ))| x,y∈V(G) ,d( x,y )=3},then the circumference of the graph G is at least min{ n,3δ *+δ,6δ }.
设 G 为n 阶3连通无爪图,δ= min{d( x)| x ∈ V( G)} ,δ= min{ max(d( x) ,d( y))| x ,y∈ V( G) ,d( x ,y) = 3} ,则 C( G) ≥min{ n ,3 δ+ δ,6 δ}·用反证法,若图 G 的最长圈不满足结论,利用 G 的3连通性和无爪性构造矛盾
5) k_(1,3)-free graph


无爪图
1.
A new sufficient condition for Hamiltonicity of K_(1,3)-free graphs;


无爪图是Hamiltonian图的一个充分条件
2.
In this paper,it is proved that let G bc a 2-connected k_(1,3)-free graph of order n,△(G)≥n-4, then G is Hamilton graph.
本文证明了:设G是n阶2-连通无爪图,△(G)≥n-4,则G是Hamilton图。
3.
Where G is a simple connected K_(1,3)-free graph and C_n is a cycle of order n.


本文通过讨论n阶圈C_n的m次幂(n>2m)给出连通无爪图的2m次幂存在m个边不交Hamilton圈的一个充分条件。
6) seedless watermelons


无籽西爪
补充资料:AutoCad 教你绘制三爪卡盘模型,借用四视图来建模型
小弟写教程纯粹表达的是建模思路,供初学者参考.任何物体的建摸都需要思路,只有思路多,模型也就水到渠成.ok废话就不说了.建议使用1024X768分辨率
开始
先看下最终效果

第一步,如图所示将窗口分为四个视图

第二步,依次选择每个窗口,在分别输入各自己的视图

第三步,建立ucs重新建立世界坐标体系,捕捉三点来确定各自的ucs如图
第四步,初步大致建立基本模型.可以在主视图建立两个不同的圆,在用ext拉升,在用差集运算.如图:

第五步:关键一步,在此的我思路是.先画出卡爪的基本投影,在把他进行面域,在进行拉升高度分别是10,20,30曾t形状.如图:

第六步:画出螺栓的初步形状.如图

第七步:利用ext拉升圆,在拉升内六边形.注意拉升六边行时方向与拉升圆的方向是相反的.
之后在利用差集运算


第八步:将所得内螺栓模型分别复制到卡爪上,在利用三个视图调到与卡爪的中心对称.效果如图红色的是螺栓,最后是差集
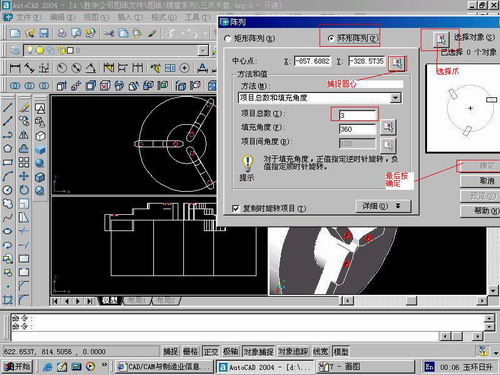
第九步:阵列

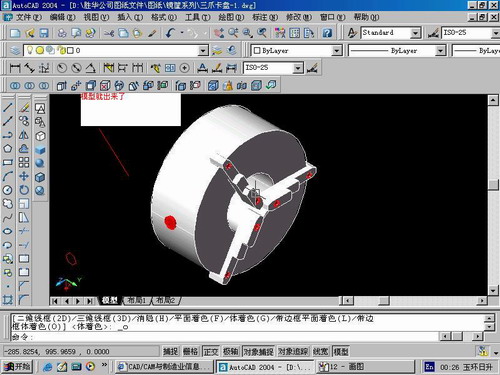
第10步.模型就完成了

来一张利用矢量处理的图片

说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条