2) Near-eigenaxis


拟欧拉轴
3) Eulerian matroid


欧拉拟阵
4) Euler angles


欧拉角
1.
In this paper, the physical singularity and computational singularity of Euler angles are investigated, then the problems encountered in defining the water-exit pose angles of the carrier areanalyzed, and anti Euler method is introduce.
研究了欧拉角定义的物理奇异性和欧拉方程求解的计算奇异性,分析了运载器垂直出水弹道姿态角定义面临的问题,提出用反欧拉法来定义和考核运载器出水弹道的姿态角。
2.
An extended Kalman filter algorithm has been developed for determining the three-axis stabilized satellite orbital attitude by Euler angles using the measurements from the typical attitude measurement system composed of vector observations and gyros.
针对“矢量观测+陀螺”这种典型的三轴稳定卫星姿态确定系统配置模式,采用欧拉角作为姿态参数,应用扩展卡尔曼滤波技术综合处理姿态测量信息,给出了具有良好滤波性能的轨道姿态估计算法。
3.
The reason why quaternion is used in flight simulation of fighter aircraft and the geometric meaning of quaternion are described,according to axis system used in flight simulation of fighter aircraft in China,three problems are introduced as follows:(1) quaternion kinematic equations,(2) relationship of quaternion and coordinate transformation matrix,(3) Euler angles in terms of quaternion.
阐述了在战斗机的飞行仿真中采用四元数的原因和四元数的几何意义,并按照中国战斗机飞行仿真中采用的坐标系,介绍了三个问题:四元数运动学方程;四元数与坐标变换矩阵的关系;用四元数表示的欧拉角。
5) euler angle


欧拉角
1.
Dynamic modeling and analysis of the spherical robot based on Euler angles description;


基于欧拉角描述下的球形机器人动力学建模与分析
2.
The formula for calculating the attitude,based on three Euler angles,was induced.


结合自动化测量机器人的功能,提出基于测量机器人对盾构体(前体)上两点进行三维坐标测量;根据安装在盾构机机体上纵、横两个精密测倾仪,实时采集的盾构机俯仰角、滚动角,来确定盾构机的实时空间位置和水平方向的偏航角的方法;根据3个欧拉角描述姿态测量的原理,推导出其姿态计算方法,并给出姿态计算的程序实现流程。
3.
Direct cosine matrix,Euler angles and quaternions are the common methods for translating vector equations into scalar equations,singularities are discussed according to equations of kinematics and geometry graph of defining Euler angles in the paper.
方向余弦阵、欧拉角法和四元数法是将导弹运动的矢量式变换到标量形式的导弹运动方程组常用的方法,文中分别通过绕质心运动的方程组和欧拉角定义的几何图形分析了欧拉角出现奇异的情形。
6) Eulerian angles


欧拉角
1.
Based on the argument that the motion of a rigid body with one point fixed can be described by the Eulerian angles,we give an alternative method of introducing the angular velocity of rigid body via calculating the velocity of an arbitrary point on the rigid body.
本文从定点运动的则体可由欧拉角来描写出发,通过计算则体上任意一点的速度来引入刚体的角速度。
补充资料:欧拉角
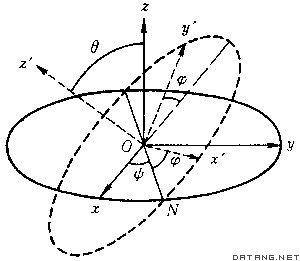
| 欧拉角 Eulerian angles 用来确定定点转动刚体位置的3个一组独立角参量,由章动角θ、旋进角(即进动角)ψ和自转角j组成。为欧拉首先提出而得名。它们有多种取法,下面是常见的一种。如图所示,由定点O作出固定坐标系Oxyz和固连于刚体的动坐标系Ox′y′z′。以轴Oz和Oz′为基本轴,其垂直面Oxy和Ox′y′为基本平面。由轴Oz量到Oz′的角θ称章动角。平面zOz′的垂线ON称节线,它又是基本平面Ox′y′和Oxy的交线。在右手坐标系中,由ON的正端看,角θ应按逆时针方向计量。由固定轴Ox量到节线ON的角ψ称旋进角;由节线ON量到动轴Ox′的角j称自转角。由轴Oz和Oz′正端看,角ψ和j也都按逆时针方向计量。若令Ox′y′z′的初始位置与Oxyz重合,经过相继绕Oz、ON和Oz′的三次转动后,刚体将转到图示的任意位置。如果刚体绕通过定点O的某一轴线以角速度ω转动,而ω在动坐标系Ox′y′z′上的投影为ωx′、ωy′、ωz′,则它们可用欧拉角及其微商表示如下:ωx′= 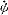 sinθsinj+ sinθsinj+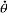 cosj,ωy′= cosj,ωy′=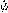 sinθcosj- sinθcosj- sinj,ωz′= sinj,ωz′=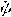 cosθ+ cosθ+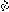 。如果已知ψ、θ、j和时间的关系,则可用上式计算ω在动坐标轴上的3个分量;反之,如已知任一瞬时t的ω各个分量,也可利用上式求出ψ、θ、j和时间t的关系,因而也就决定了刚体的运动。上式通常被称为欧拉运动学方程。 。如果已知ψ、θ、j和时间的关系,则可用上式计算ω在动坐标轴上的3个分量;反之,如已知任一瞬时t的ω各个分量,也可利用上式求出ψ、θ、j和时间t的关系,因而也就决定了刚体的运动。上式通常被称为欧拉运动学方程。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条