1) elementary transformation of similitude


初等相似变换
1.
In this paper, the concept of elementary transformation of similitude is proposed, and the method how to find the Jordan canonical form of a square matrix and its transformation matrix are studied.
文章提出了初等相似变换的概念 ,探讨了如何利用初等相似变换法求一个方阵的Jordan标准形及变换矩阵 ,进而为求一个方阵的广义特征向量创造了条件。
2) Elementary transformation


初等变换
1.
Improvement on the elementary transformation method of QR decomposition of matrix;


矩阵QR分解初等变换法的改进
2.
Application of elementary transformation of matrix;


矩阵初等变换的一个应用
3.
Finding bases for sum and intersection of subspaces in Pn using elementary transformations;
利用初等变换求P~n中子空间的和与交的基
3) elementary operation


初等变换
1.
A method of seeking Moore-Penrose s generalized inverse metrix through elementary operation;
求Moore-Penrose广义逆的初等变换法
2.
This paper presents an approach to find out the matrix eigenvalue and eigenvector of an eigenmatrix using elementary operations, which is an easier and quicker way to obtain the similarity diagonalization of a matrix.
文章针对特征矩阵施行初等变换,提出了求出矩阵特征值和特征向量的一种方法,从而以简捷的方式将矩阵相似对角化。
3.
In this paper, a practical solving method and an expression of general solution of a matrix equation AXB=CYD are given by using matrix techniques and elementary operations on matrix.
应用矩阵的初等变换技巧 ,给出了任意域上矩阵方程AXB =CYD的通用表达式及解法。
4) elementary operations


初等变换
1.
Matrix equations under elementary operations;


初等变换下的矩阵方程AX=B
2.
In the paper , we gives a condition and an expression of general solution of a matrix equation AXB=C by using some matrix techniques and elementary operations on matrices.
文章应用矩阵的初等变换等技巧 ,给出了任意域上矩阵方程AXB =C的有解条件、实用解法及通解。
3.
In the paper,by using some matrix techniques and elementary operations on matrix equations,we give a condition and an expression of general solution of two kinds of matrix equations ABX= CYD, AXB = C.
文章应用矩阵的初等变换、矩阵分解等技巧,给出了任意域上两类矩阵方程AXB=CYDAXB=C的解法及通用表达式。
5) primary transformation


初等变换
1.
The way of solving matrix equation directly with primary transformation method is discussed with the premise of the matrix of coefficients being reversible, which makes the solving procedures more simple.
讨论了在系数矩阵可逆的前提下 ,如何用初等变换的方法直接求解矩阵方程 ,使求解过程更简化 ,同时给出一般线性方程组的初等变换直观解
2.
A simple method of solving an orthogonal transformation with a primary transformation is presented by change quadric form into canonical form.
给出了利用初等变换求一个正交变换化实二次型为标准形的简便方
3.
Results Getting the effective way of selecting the proper primary matrix from the primary transformation.
方法利用矩阵的初等变换。
6) Primary transform


初等变换
1.
The primary transform is used to solve a lot of important questions, such as finding matrix inversion and standard form.
以初等变换为首要方法,解决线性代数中一类重要问题。
2.
By using primary transform of matrices we have proposed a new method for solving the singular systems EX=AX + Bu.
本文利用矩阵的初等变换技巧,对广义系统EX=AH+BU的解给出了一种新的计算方法。
补充资料:初等几何变换
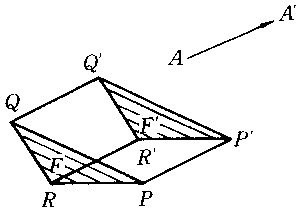
| 初等几何变换 elementary geometric transformation 将几何图形按某种法则或规律变成另一个几何图形的过程。几何图形是点的集合,所以几何变换就是两个图形点之间的一一对应,即点变换。它在几何学中有重要的作用。初等几何变换在平面上主要有全等变换、相似变换和反演变换。 全等变换 它是平面上的点到其自身的一个一一对应,使其中任意两点A、B间的距离与其对应点A′、B′间之距离相等即|AB|=|A′B′|。两点间的距离是全等变换的基本不变量。全等变换也称等距变换或合同变换。图形经全等变换后与其对应图形是相等的(真正相等或镜像相等)。全等变换的特殊情况有平移变换、旋转变换和轴反射变换。平面上把每点P 按定向量AA′的方向移到点P′,使|PP′|=|AA′|的变换称为沿向量AA′的平移变换(图1),简称平移变换或平移。在平移变换下,图形F的任意两点P、Q与其对应点P′、Q′所连线段平行且相等,故平移变换把一个图形变到与其真正相等的图形。
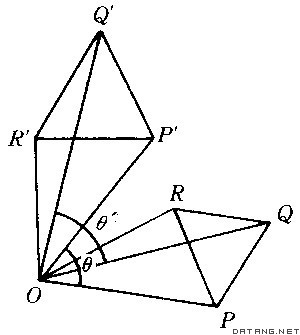
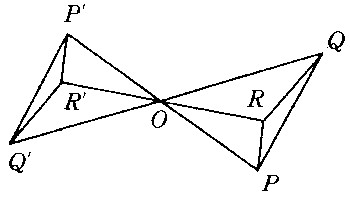
平面上把每一个点P绕定点O旋转一定角θ变到点P′的变换称为绕着定点的旋转变换,简称为旋转(图2),定点O称为旋转中心,定角θ称为旋转角。在旋转变换下|OP|=|OP′|,∠POP′=θ,图形F中的任意两点P、Q与其对应两点P′Q′所连线段必相等。旋转变换把一个图形变到与其真正相等的图形。特别地,当θ=0时,即为恒等变换(每点的对应点均为其自身的变换)。当θ=π时,称为中心反射(图3),旋转中心称为反射中心。如果一个图形在某一中心反射下的对应图形为其自身,则称为中心对称图形,如平行四边形、圆、椭圆、双曲线均是中心对称图形。
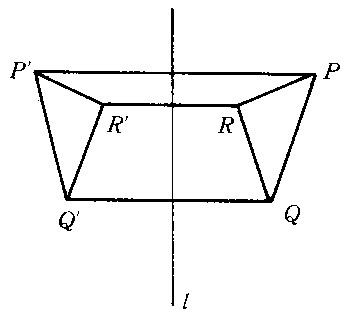
平面上任意一点P,若P在定直线l上,则规定其为自对应点,若P不在l上,则规定P与其对应点P′所连线段PP′被定直线l垂直平分,即P与P′对于l是对称点,这样的变换称为轴反射变换(图4)。定直线L称为反射轴。轴反射变换把一个图形变到与它对称相等的图形。在同一平面内,对于连续两次轴反射变换,当两反射轴重合时,则为恒等变换;当两反射轴平行时,则为平移变换;当两反射轴相交时,则为旋转变换。
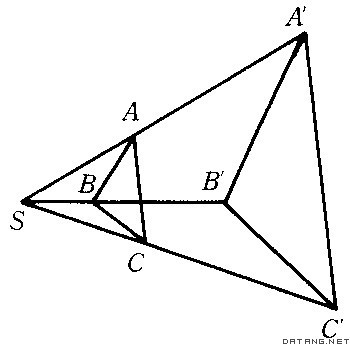
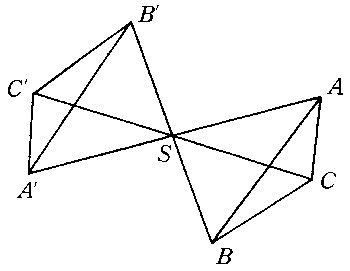
相似变换 它是平面上点的一一对应,使对于任意两点A、B与它的对应点A′、B′间有A′B′=λAB,(λ是正常数),当λ=1时,即为全等变换。相似变换的特殊情况是位似变换,即平 面上点的一一对应,使任意点A及其对应点A′对于定点S,总有①S、A、A′三点共线 ;②SA′=|λ|SA(λ≠0),称之为以S为位似中心,λ为位似比的位似变换(图5)。当λ>0时,A与其对应点A′在位似中心S的同侧;当λ<0时,A与A′在点S的两侧。当|λ|>1时,原图形被放大;当|λ|<1时,原图形被缩小。特别地,当λ=1时,即为以S为中心,旋转角为π的旋转变换(图6)。
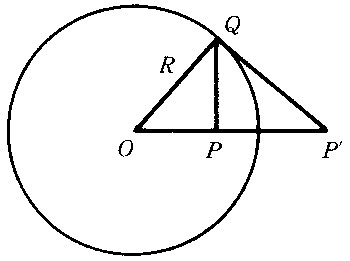
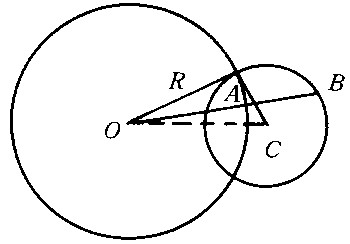
反演变换 它是平面上点的一一对应,对于已知中心在点O,半径为R的圆,使异于O的任一点P与其对应点P′间总有O、P、P′三点共线,且OP·OP′=R2。称P′为P的反演点,O为反演中心,R为反演半径或反演幂,所给的圆为反演基圆(图7)。反演变换具有以下性质:①P与P′互为反演点;②反演圆上每点的反演点为其自身,反演圆内部的点变到圆外部的点;反之,圆外点变到圆内点;③通过反演中心的直线的反演为其自身,通过反演中心的圆的反演为不通过反演中心的直线;④不通过反演中心的圆的反演仍为一圆;⑤反演中心的反演为平面上的无穷远点;⑥两圆的交角等于反演变成的两圆的交角(即反演是保角变换);⑦一圆若非反演圆,它的反演为其自身的必要充分条件是它与其反演圆正交(图8)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条