1) elementary row transformation


初等行变换
1.
Knowledge reduction algorithm based on elementary row transformation of Boolean matrix;


基于布尔矩阵的初等行变换的知识约简算法
2.
Two definitions called discernible Boolean matrix of consistent decision table and elementary row transformation of Boolean matrix are given.
提出协调决策表的可辨识布尔矩阵和布尔矩阵的初等行变换的概念,建立属性约简的数学模型。
3.
The paper makes an introduction to the applications of elementary row transformation in the solution to the ranks of matrix, finding inverse matrix,resolving matrix equation and linear equations and linear relations among vector.
本文介绍了矩阵的初等行变换在求矩阵的秩、求可逆矩阵的逆矩阵、解矩阵方程、解线性方程组以及研究向量间的 线性关系等方面的应用。
2) elementary row operation


初等行变换
1.
The method is that make use of row vector as matrix and then change matrix by performing elementary row operation.
本文通过几个反例说明了在求向量组的极大无关组时,以往普遍使用的以向量为行向量作矩阵,再对矩阵作初等行变换的方法是不完善的,甚至会导致错误的结果。
2.
Based on matrix s elementary row operation remaining its column vector s linear relationship and Hermite standard form of matrix,the paper gives a simple method for solving full rank decomposition of matrix only through elementary row operation.
利用矩阵初等行变换不改变矩阵列向量组线性关系的性质,以及矩阵的Hermite标准形,给出了一种只通过初等行变换可求得矩阵满秩分解的简单方法。
3.
This paper discussed orthonormalization of linearly independent vectors and found two methods of orthonormaliztion using elementary row operation of vector matrix.
通过讨论得到利用向量矩阵的初等行变换和将线性无关向量组进行规范正交化的两种方法。
3) elementary transformation


初等行变换
1.
The method makes use of an elementary transformation of mastrix to find the solution of an invertible matrix.
给出了利用矩阵的初等行变换求可逆矩阵的伴随矩阵的一种简便方法。
4) elementary line transformation


初等行变换
1.
In the solving process of homogeneous equation set,the operational procedure for elementary line transformation is sometimes not simple and convenient as it seems to be.
在齐次方程组求解的过程中,初等行变换的运算过程有时显得并不简便。
5) row elementary operation


行初等变换
1.
The brief proof is given for "row elementary operations keep the linear relationship of column vectors of matrix",by using multiplication of partitioned matrix and the relation between elementary matrix and elementary operation.
利用初等矩阵与初等变换的对应关系及分块矩阵的乘法,给出矩阵的行初等变换不改变其列向量组的线性关系"的一个简易证明。
2.
A new method of calculating the greatest common divisor of several integers by using the row elementary operation is given.
利用整数矩阵的行初等变换给出一种求几个整数的最大公因数的新方法,并给出这种方法的一个应用。
6) line elementary transformation


行初等变换
1.
At first,the writer introdues briefly the way of evaluating invertible matrix s inverse with column elementary transformation,then emphatically introduces the other way of evaluating invertible matrix s inverse mixed use of line elementary transformation,column elementary transformation,and can solve the invertible matrix s linear equations of matrix of coefficients.
先扼要介绍列初等变换求可逆矩阵的逆的方法 ,然后着重介绍行初等变换、列初等变换的混合使用同样可以求逆矩阵的逆 ,并且能解系数矩阵为可逆矩阵的线性方程
补充资料:初等几何变换
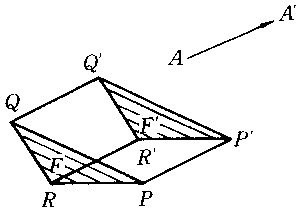
| 初等几何变换 elementary geometric transformation 将几何图形按某种法则或规律变成另一个几何图形的过程。几何图形是点的集合,所以几何变换就是两个图形点之间的一一对应,即点变换。它在几何学中有重要的作用。初等几何变换在平面上主要有全等变换、相似变换和反演变换。 全等变换 它是平面上的点到其自身的一个一一对应,使其中任意两点A、B间的距离与其对应点A′、B′间之距离相等即|AB|=|A′B′|。两点间的距离是全等变换的基本不变量。全等变换也称等距变换或合同变换。图形经全等变换后与其对应图形是相等的(真正相等或镜像相等)。全等变换的特殊情况有平移变换、旋转变换和轴反射变换。平面上把每点P 按定向量AA′的方向移到点P′,使|PP′|=|AA′|的变换称为沿向量AA′的平移变换(图1),简称平移变换或平移。在平移变换下,图形F的任意两点P、Q与其对应点P′、Q′所连线段平行且相等,故平移变换把一个图形变到与其真正相等的图形。
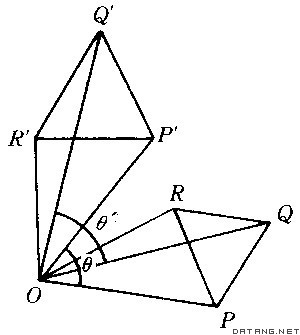
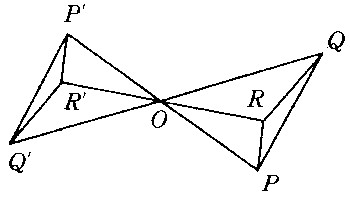
平面上把每一个点P绕定点O旋转一定角θ变到点P′的变换称为绕着定点的旋转变换,简称为旋转(图2),定点O称为旋转中心,定角θ称为旋转角。在旋转变换下|OP|=|OP′|,∠POP′=θ,图形F中的任意两点P、Q与其对应两点P′Q′所连线段必相等。旋转变换把一个图形变到与其真正相等的图形。特别地,当θ=0时,即为恒等变换(每点的对应点均为其自身的变换)。当θ=π时,称为中心反射(图3),旋转中心称为反射中心。如果一个图形在某一中心反射下的对应图形为其自身,则称为中心对称图形,如平行四边形、圆、椭圆、双曲线均是中心对称图形。
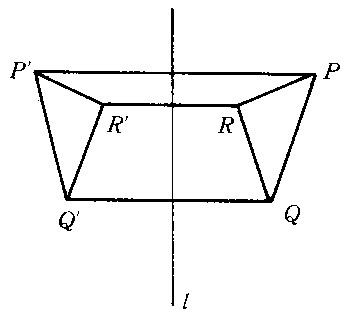
平面上任意一点P,若P在定直线l上,则规定其为自对应点,若P不在l上,则规定P与其对应点P′所连线段PP′被定直线l垂直平分,即P与P′对于l是对称点,这样的变换称为轴反射变换(图4)。定直线L称为反射轴。轴反射变换把一个图形变到与它对称相等的图形。在同一平面内,对于连续两次轴反射变换,当两反射轴重合时,则为恒等变换;当两反射轴平行时,则为平移变换;当两反射轴相交时,则为旋转变换。
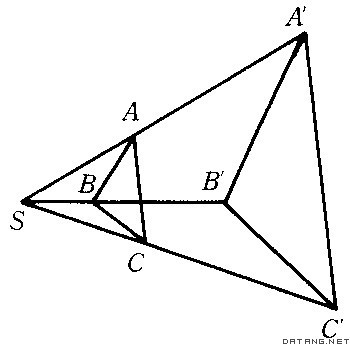
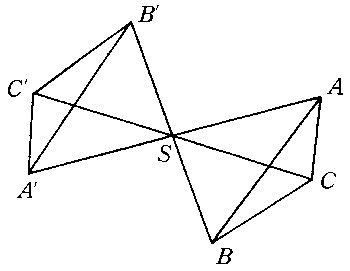
相似变换 它是平面上点的一一对应,使对于任意两点A、B与它的对应点A′、B′间有A′B′=λAB,(λ是正常数),当λ=1时,即为全等变换。相似变换的特殊情况是位似变换,即平 面上点的一一对应,使任意点A及其对应点A′对于定点S,总有①S、A、A′三点共线 ;②SA′=|λ|SA(λ≠0),称之为以S为位似中心,λ为位似比的位似变换(图5)。当λ>0时,A与其对应点A′在位似中心S的同侧;当λ<0时,A与A′在点S的两侧。当|λ|>1时,原图形被放大;当|λ|<1时,原图形被缩小。特别地,当λ=1时,即为以S为中心,旋转角为π的旋转变换(图6)。
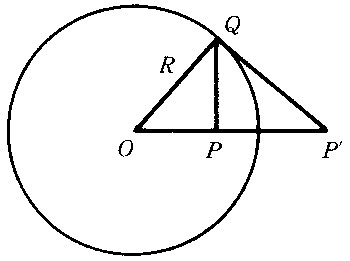
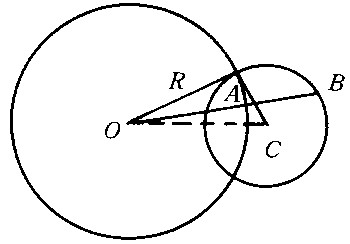
反演变换 它是平面上点的一一对应,对于已知中心在点O,半径为R的圆,使异于O的任一点P与其对应点P′间总有O、P、P′三点共线,且OP·OP′=R2。称P′为P的反演点,O为反演中心,R为反演半径或反演幂,所给的圆为反演基圆(图7)。反演变换具有以下性质:①P与P′互为反演点;②反演圆上每点的反演点为其自身,反演圆内部的点变到圆外部的点;反之,圆外点变到圆内点;③通过反演中心的直线的反演为其自身,通过反演中心的圆的反演为不通过反演中心的直线;④不通过反演中心的圆的反演仍为一圆;⑤反演中心的反演为平面上的无穷远点;⑥两圆的交角等于反演变成的两圆的交角(即反演是保角变换);⑦一圆若非反演圆,它的反演为其自身的必要充分条件是它与其反演圆正交(图8)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条