1) Gaussian mixture model-universal background model(GMM-UBM)


Gauss混合模型-通用背景模型(GMM-UBM)
2) GMM-UBM model


GMM-UBM模型
3) Gaussian Mixture Model-Universal Background Model


高斯混合-通用背景模型
4) Gaussian Mixture Model-Universal Background Model (GMM-UBM)


高斯混合模型-通用背景模型
5) Gaussian mixture model (GMM)


高斯混合模型(GMM)
6) Gaussian mixture model(GMM)


高斯混合模型(GMM)
1.
Support vector machines(SVM) and Gaussian mixture model(GMM) are widely applied to the speaker verification,but they both have the disadvantages.
阐述高斯混合模型(GMM)和支持向量机(SVM)建立的基本原理,分别指出高斯混合模型和支持向量机在实际应用中的不足之处,并针对两种模型的特点,提出将GMM模型的输出机制引入到SVM模型中,以便于调整支持向量机(SVM)模型的概率输出,并建立SVM-GMM混合模型。
补充资料:模型
| 模型 model 能给出逻辑公式取值的一种泛代数结构。一个泛代数是指一个具有若干运算、关系及特指元素的非空集合。一个模型A由4个部分组成:一个非空个体集合A,A也叫论域;论域A上的关系;A上的函数;A中指定的个体常元。如果L是一阶语言,L中的关系,函数和常量符号在模型A中都有相应的关系,函数和常量分别作他们的解释,就称A是L的模型,指定A中一些元素作L的变元符号 v0,v1… 的解释,称为一个指派式赋值。在一定的指派下,L中每个项就都有了A中指定的元素作解释。给定一个指派,L中的原子公式(见一阶公式)t1≡t2在模型A中取值为真当且仅当t1,t2在A中的解释相同 ;原子公式R(t1,…tn)在A中取值为真当且仅当(t1…tn)在A中的解释满足R在A中的解释。L的公式 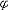 在模型A中的取值可以归纳地定义: 在模型A中的取值可以归纳地定义: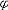 是原子公式已定义;如果 是原子公式已定义;如果 = = ψ,则 ψ,则 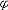 取值真当且仅当ψ取值假;如果 取值真当且仅当ψ取值假;如果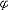 =ψ1 =ψ1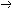 ψ2,则 ψ2,则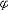 取值真当且仅当ψ1取值假,ψ2取值真。如果 取值真当且仅当ψ1取值假,ψ2取值真。如果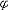 ="xψ,则 ="xψ,则 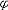 取值真当且仅当用论域A中任意一个元素解释变元x时,ψ取值真。这就是一阶逻辑的基本语义定义。由这个定义,只要对 取值真当且仅当用论域A中任意一个元素解释变元x时,ψ取值真。这就是一阶逻辑的基本语义定义。由这个定义,只要对 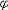 中的自由变元给出A中一定的元素作解释, 中的自由变元给出A中一定的元素作解释,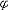 的取值就唯一确定。如果 的取值就唯一确定。如果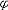 是没有自由变元(见一阶公式)的句子 , 是没有自由变元(见一阶公式)的句子 ,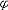 在一个模型中就有唯一确定的真假值。句子 在一个模型中就有唯一确定的真假值。句子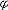 在模型A中取值为真 ,就称A是句子 在模型A中取值为真 ,就称A是句子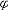 的模型。 的模型。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条