1) neutron transport equation


中子输运方程
1.
An approximate linearization method is proposed for nonlinear neutron transport equations.
针对考虑中子之间相互碰撞的非线性中子输运方程,提出一种线性化近似处理方法,导出相应的积分输运方程,利用蒙特卡罗方法求解此方程,数值实验表明算法的有效性,为研究超高能中子产生与输运问题提供了必要的模拟工具。
2.
In this paper the methods of determining iterative initial value about iterative proce- dure for discrete ordinate time-dependent neutron transport equation are studied.
研究离散纵标动态中子输运方程迭代求解时,迭代初值的不同选取方法,设计合理的迭代初值可以适当放宽对时间步长的限制,缩短计算时间。
3.
Motivated by issues from applications and requirements in the future, this paper is focused on the numerical simulations for the multi-dimensional neutron transport equation.
针对高维中子输运方程的数值模拟,基于在应用中提出的问题和未来发展的需求,本文研究了二维离散格式的“对称性”问题,并对三维差分方程作了离散解的先验估计以及并行和加速收敛算法的设计、应用,得到了若干具有理论和实际意义的成果。
2) 2-D neutron transport equation


二维中子输运方程
1.
The 2-D neutron transport equation is one of the most important partial differential equations used in scientific computing.
二维中子输运方程是科学计算中的一类重要的偏微分方程,其数值求解的计算量非常巨大,通常采用并行化的方法求解。
3) homogeneous neutron transport equation


齐次中子输运方程
4) one-velocity neutron transport equation


单速中子输运方程
5) neutron transport equation


中子迁移方程;中子输运方程
6) particle transport equation


粒子输运方程
1.
A linear discontinuous spatial finite element scheme for time-dependent particle transport equation is studied.
将空间线性间断有限元方法应用于动态粒子输运方程的求解。
补充资料:玻耳兹曼输运方程
| 玻耳兹曼输运方程 Boltzmann's transport equation 含时间的分布函数的演化方程,是讨论输运过程的基本方程。因方程中既有积分又有微分,故又称玻耳兹曼积分微分方程。 若将速度在v和(v+dv) 之间、坐标在r和(r+dr)之间的分子数目在总分子数中所占比率(即百分数)表为f(r,v,t)drdv,则f( r,v,t) 称为非平衡态的分布函数,它随时间变化。1872年玻耳兹曼把分布函数的变化率 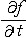
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |