1) PDF transport equation method


PDF输运方程方法
2) PDF transport equation


PDF输运方程
3) PDF equation


PDF方程
1.
In this paper, using the method of state vector expanding color-noise system for color-noise system, the joint PDF equation of particle position-particle velocity-fluid velocity is gained, and the PDF equation of particle position- velocity is also o.
在此基础之上发展了“有限解析/MC数值方法”:将“扩维方法”得到的两相流PDF输运方程约化到速度空间,在某个固定物理位置上解析地解出速度PDF方程,再跟踪随机颗粒,统计获得两相流场;然后应用此方法对壁面两相射流进行数值模拟,求解结果与实验结果进行对比分析。
4) PDF method


PDF方法
1.
In the PDF method, the reactive scalars are obtained through the computation of their PDF transport equation, whereas in the flamelet models, only a single scalar mixture fraction PDF equation is solved and reactive scalars are gained by solving the flamelet .
PDF方法通过计算反应标量的PDF输运方程来得到标量分布,而火焰面模型只求解单标量混合物分数的PDF方程,组分和温度分布通过火焰面方程的求解或者火焰面数据库的插值得到。
5) transport equation


输运方程
1.
This paper systematically studies the finite-element method of solving the Galerkin variation problem of the transport equation in well-logging condition and developed a finite-element mesh program which can be used in 2-dimension and 3-dimension well-logging domain.
在测井条件下,系统研究了输运方程的Galerkin变分问题的有限元求解过程。
2.
The transport equation of air age is derived based on tracer gas technique.


为了替代示踪气体方法评价室内空气品质和通风有效性,在示踪气体研究方法的基础上,推导出空气年龄的输运方程,用计算流体力学的方法对该方程进行了求解。
3.
In the frame of multigroup P_1 approximation the neutron transport equation is soluted by using finite-element method and the two-dimentional finite-element code FEMLOG is devel- oped for the numerical simulation of neutron well-logging.
用有限元方法求解多群 P_1近似中子输运方程,编制了二维有限元程序 FEMLOG,并对中子测井问题进行了数值计算。
6) transport equations


运输方程
1.
In the first one,our aim is to prove the existence of a flow of measurable maps associated to a vector field belonging to a Sobolev space;to this end,we discuss the link with transport equations and continuity equations.
在第一部分中,我们的目的是证明由属于Sobolev空间的向量场生成的可测映射流的存在性,为此我们讨论常微与运输方程和连续方程的联系。
补充资料:玻耳兹曼输运方程
| 玻耳兹曼输运方程 Boltzmann's transport equation 含时间的分布函数的演化方程,是讨论输运过程的基本方程。因方程中既有积分又有微分,故又称玻耳兹曼积分微分方程。 若将速度在v和(v+dv) 之间、坐标在r和(r+dr)之间的分子数目在总分子数中所占比率(即百分数)表为f(r,v,t)drdv,则f( r,v,t) 称为非平衡态的分布函数,它随时间变化。1872年玻耳兹曼把分布函数的变化率 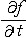
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |